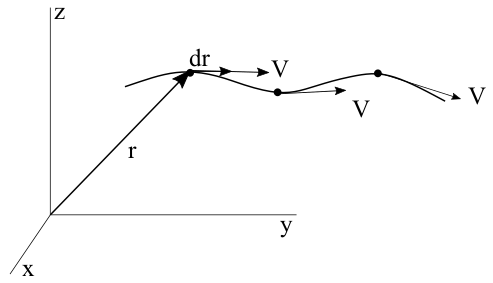
A velocity field is given by V=3yt\hat{i}+5x\hat{j}. Find the equation of the streamline passing through the point (5,3) at t =3. Units of x,y are in meters and time-t is in seconds.
A velocity field is given by V=3yt\hat{i}+5x\hat{j}. Find the equation of the streamline passing through the point (5,3) at t =3. Units of x,y are in meters and time-t is in seconds.
Velocity field is V=\left ( 3yt\hat{i}+5x\hat{j} \right )
In a streamline flow, velocity is tangent to the flow. V and dr is in the same direction. Therefore,
V\times dr=0Since, two vectors are in the same direction, their cross product is 0.
V\times dr = 0\Rightarrow \left ( 3yt\hat{i}+5x\hat{j} \right )\times \left ( dx\hat{i}+dy\hat{j} \right )=0
\Rightarrow \begin{vmatrix} \hat{i} &\hat{j} &\hat{k} \\ 3yt& 5x &0 \\ dx&dy & 0 \end{vmatrix}=0
\Rightarrow \hat{k}\left ( 3ytdy-5xdx \right )=0
At, time t = 3
\Rightarrow 9y\left ( 3 \right )dy -5xdx=0\Rightarrow 9ydy -5xdx=0\Rightarrow 9ydy=5xdx
On integrating
\Rightarrow \int 9ydy=\int 5xdx
\Rightarrow 9\int ydy=5\int xdx
\Rightarrow 9\frac{y^{2}}{2}+c_{1}=\frac{5x^{2}}{2}+c_{2}
\Rightarrow \frac{9y^{2}+2c_{1}}{2}=\frac{5x^{2}+2c_{2}}{2}
\Rightarrow 9y^{2}+2c_{1}=5x^{2}+2c_{2}
\Rightarrow 9y^{2}-5x^{2}=2c_{2}-2c_{1}
\Rightarrow 9y^{2}-5x^{2}=C
In a streamline flow, velocity is tangent to the flow. V and dr is in the same direction. Therefore,
V\times dr=0Since, two vectors are in the same direction, their cross product is 0.
V\times dr = 0\Rightarrow \left ( 3yt\hat{i}+5x\hat{j} \right )\times \left ( dx\hat{i}+dy\hat{j} \right )=0
\Rightarrow \begin{vmatrix} \hat{i} &\hat{j} &\hat{k} \\ 3yt& 5x &0 \\ dx&dy & 0 \end{vmatrix}=0
\Rightarrow \hat{k}\left ( 3ytdy-5xdx \right )=0
At, time t = 3
\Rightarrow 9y\left ( 3 \right )dy -5xdx=0\Rightarrow 9ydy -5xdx=0\Rightarrow 9ydy=5xdx
On integrating
\Rightarrow \int 9ydy=\int 5xdx
\Rightarrow 9\int ydy=5\int xdx
\Rightarrow 9\frac{y^{2}}{2}+c_{1}=\frac{5x^{2}}{2}+c_{2}
\Rightarrow \frac{9y^{2}+2c_{1}}{2}=\frac{5x^{2}+2c_{2}}{2}
\Rightarrow 9y^{2}+2c_{1}=5x^{2}+2c_{2}
\Rightarrow 9y^{2}-5x^{2}=2c_{2}-2c_{1}
\Rightarrow 9y^{2}-5x^{2}=C
At, point (5,3), since,
9y^{2}-5x^{2}=C\Rightarrow C= 9\left ( 3 \right )^{2}-5\left ( 5 \right )^{2}\Rightarrow C=\left ( 9\times 9 \right )-\left ( 5\times 25 \right )\Rightarrow C=81-125=-44Therefore, the equation of the streamline is,
9y^{2}-5x^{2}=-44\Rightarrow 9y^{2}-5x^{2}+44=0