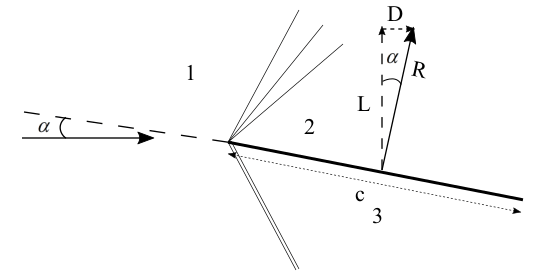Supersonic flow over a thin flat plate at an angle of attack

From the $\theta -\beta -M$ relationship, for $\theta = 8^{\circ}$ and $M = 3$, $\beta =25.611^{\circ}$
Therefore,
$$M_{n1}=M_{1}Sin\beta =3Sin\left ( 25.611^{\circ} \right )=1.297$$
From normal shock properties, for $M_{n1}=1.297$, $\frac{p_{3}}{p_{1}}=1.796$
From isentropic flow properties, for $M_{1}=3$, $\left ( \frac{p_{1}}{p_{01}} \right )=0.02722$
From prandtl-Meyer function for $M_{1}=3$, $\nu _{1}=49.76$
Therefore, $$\nu _{2}=\nu _{1}+\theta =49.76^{\circ}+8^{\circ}=57.76^{\circ}$$
For, $\nu _{2}=57.76^{\circ}, M_{2}=3.452$

For, $M_{2}=3.452$, from isentropic flow properties
$$\left ( \frac{p_{2}}{p_{02}} \right )=0.01404$$

Therefore,
$$\frac{p_{2}}{p_{1}}=\left ( \frac{p_{2}}{p_{02}} \right ) \left ( \frac{p_{02}}{p_{01}} \right )\left ( \frac{p_{01}}{p_{1}} \right )=\left ( 0.01404 \right ) \left ( 1 \right )\left ( \frac{1}{0.02722} \right )=0.5158$$

Total pressure is constant through the expansion wave, $p_{02}=p_{01}$.
For, a thin flat plate lift per unit span is $L{}’=\left ( p_{3}-p_{2} \right )\left ( c \right )cos\alpha$

also, $$c_{l}=\frac{L{}’}{q_{1}S} =\frac{L{}’}{\frac{\gamma }{2}p_{1}M_{1}^{2}c} =\frac{\left ( p_{3}-p_{2} \right )\left ( c \right ) cos\alpha }{\frac{\gamma }{2}p_{1}M_{1}^{2}c} =\frac{2}{\gamma M_{1}^{2}}\left ( \frac{p_{3}}{p_{1}}-\frac{p_{2}}{p_{1}} \right )cos\alpha$$
$$\Rightarrow c_{l}=\frac{2}{\left ( 1.4 \right )\left ( 3^{2} \right )}\left ( 1.796-0.5158 \right )cos\left ( 8^{\circ} \right )=0.20123$$

For a thin flat plate, drag per unit span is $D{}’=\left ( p_{3}-p_{2} \right )\left ( c \right )sin\alpha$
also,
$$c_{d}=\frac{D{}’}{q_{1}S}=\frac{D{}’}{\frac{\gamma }{2}p_{1}M_{1}^{2}c} =\frac{\left ( p_{3}-p_{2} \right )\left ( c \right ) sin\alpha }{\frac{\gamma }{2}p_{1}M_{1}^{2}c} =\frac{2}{\gamma M_{1}^{2}} \left ( \frac{p_{3}}{p_{1}}-\frac{p_{2}}{p_{1}} \right )sin\alpha$$
$$\Rightarrow c_{d}=\frac{2}{\left ( 1.4 \right )\left ( 3^{2} \right )}\left ( 1.796-0.5158 \right )sin\left ( 8^{\circ} \right )=0.02828$$