Oblique Shock wave on a wedge

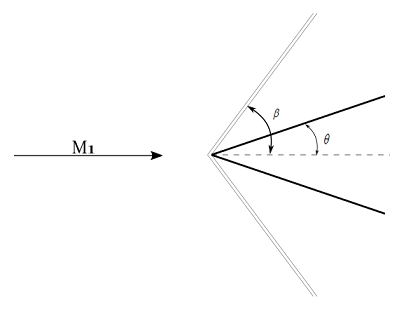
Wave angle can be found from \(\theta -\beta -M\)  diagram. For deflection angle \(\theta =20^{\circ}\)  and Mach number, \(M_{1}=2.8\) , wave angle \(\beta =39.5^{\circ}\).

Therefore, normal component of upstream Mach number,

\[M_{n1}=M_{1}Sin\beta = 2.8Sin\left ( 39.5^{\circ} \right )=1.78\]

From normal shock properties table, for \(M_{n1}=1.78\),

\(\frac{p_{2}}{p_{1}}=3.530,\frac{T_{2}}{T_{1}}=1.517,M_{n2}=0.6210\)

Therefore, Downstream pressure, \[ p_{2}=\left ( \frac{p_{2}}{p_{1}} \right )p_{1}=\left ( 3.530 \right )\left ( 1\,atm \right )=3.53\,atm\]

Downstream temperature, \[T_{2}=\left ( \frac{T_{2}}{T_{1}} \right )T_{1}=\left ( 1.517 \right )310=470.27\,K\]

Downstream Mach number, \[ M_{2}=\frac{M_{n2}}{sin\left ( \beta -\theta \right )}=\frac{0.6210}{Sin\left ( 39.5-20 \right )}=1.86\]

Orbital velocity: It is the velocity acquired by an object to orbit around any celestial body. The orbital path is a balance between gravity of the celestial body and inertia to move in a straight line of the object.

Escape velocity: It is the velocity of an object to overcome or escape the gravitational force of a planet and enter into orbit. Orbital velocity is given as

\[{V_{orbital}} = \sqrt {\frac{{G{M_{earth}}}}{r}} \]

Here,

\[G{M_{earth}} = \left( {6.67 \times {{10}^{ – 11}}} \right)\left( {5.9722 \times {{10}^{24}}} \right) = 3.98 \times {10^{14}}\,{m^3}/{s^2}\]

Therefore,

\[{V_{orbital}} = \sqrt {\frac{{3.98 \times {{10}^{14}}}}{{6.378 \times {{10}^6}}}} = 7899.494\,m/s = 7.9\,km/s\]

Escape velocity is \(\sqrt 2 \) orbital velocity,

Therefore,

\[{V_{escape}} = \sqrt 2 {V_{orbital}} = \sqrt 2 \times 7899.494\,m/s = 11171.572\,m/s = 11.2\,km/s\]

At an altitude of 55 km, ambient pressure, \({p_\infty } = 48.4\,N/{m^2}\)

Thrust produced by a rocket engine is given by

\[T = \dot m{V_e} + \left( {{p_e} – {p_\infty }} \right){A_e}\]

\[ \Rightarrow T = \left( {30 \times 4500} \right) + \left( {2.2 \times {{10}^4} – 48.4} \right)2.5 = 189879\,N\]

Expansion waves are formed when there is a supersonic flow over a curved surface or a convex corner. Expansion waves on a convex corner are in the shape of a fan with its center at the corner.

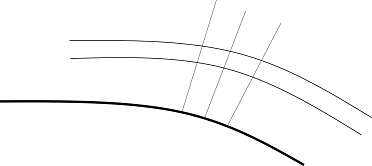Expansion wave formed over a curved surface

Flow passing the expansion waves are deflected by deflection angle, \(\theta\), and streamlines of the flow are parallel to each other. The expansion fan has an infinite number of Mach waves which diverges from the sharp corner. These Mach waves make an angle, \(\mu \), with the local flow direction. The first Mach wave is at an angle of \({\mu _1} = {\sin ^{ – 1}}\left( {\frac{1}{{{M_1}}}} \right).\) with respect to the flow direction. The last Mach wave is at an angle of \({\mu _2} = {\sin ^{ – 1}}\left( {\frac{1}{{{M_2}}}} \right).\)

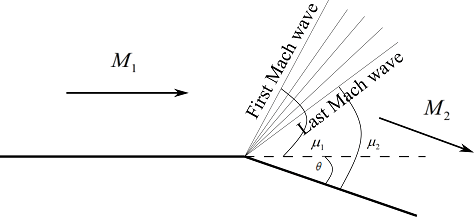Expansion fan formed over a convex corner

Across an expansion wave pressure, temperature and density decreases where as Mach number increases. The deflection angle, \(\theta\), of the flow can be calculated from Prandtl-Meyer function, \[\theta = \nu \left( {{M_2}} \right) – \nu \left( {{M_1}} \right)\]

where,

\[\nu \left( M \right) = \sqrt {\frac{{\gamma + 1}}{{\gamma – 1}}} {\tan ^{ – 1}}\sqrt {\frac{{\gamma – 1}}{{\gamma + 1}}\left( {{M^2} – 1} \right)} – {\tan ^{ – 1}}\sqrt {{M^2} – 1} \]

At an altitude of \(10 000\, m\) , temperature and density are \({T_\infty } = 223.26K,{\rho _\infty } = 0.41351kg/{m^3}\). Speed of sound , at this altitude will be 

\[{a_\infty } = \sqrt {\gamma R{T_\infty }} = \sqrt {1.4 \times 287 \times 223.26} = 299.51m/s\]

Therefore, velocity of the airplane is 

\[{V_\infty } = {M_\infty }{a_\infty } = 2.1 \times 299.51 = 628.971m/s\]

For, a level flight, Lift = Weight,

\[L = \frac{1}{2}{\rho _\infty }V_\infty ^2S{C_L} \Rightarrow {C_L} = \frac{L}{{\frac{1}{2}{\rho _\infty }V_\infty ^2S}} = \frac{{70000}}{{\frac{1}{2} \times 0.41351 \times {{\left( {628.971} \right)}^2} \times 20}} = 0.04279\]

Lift coefficient for a flat plate in a supersonic flow is,

\[{C_L} = \frac{{4\alpha }}{{\sqrt {M_\infty ^2 – 1} }}\]

\[ \Rightarrow \alpha = \frac{1}{4}{C_L}\sqrt {M_\infty ^2 – 1} = \frac{1}{4} \times 0.04279 \times \sqrt {{{2.1}^2} – 1} = 0.01975\,radians\]

Wave drag coefficient for a flat plate in a supersonic flow is

\[{C_{{D_w}}} = \frac{{4{\alpha ^2}}}{{\sqrt {M_\infty ^2 – 1} }} = \frac{{4 \times {{\left( {0.01975} \right)}^2}}}{{\sqrt {{{2.1}^2} – 1} }} = 0.00084\]

Therefore, wave drag on the wings of the airplane is

\[{D_w} = \frac{1}{2} \times {\rho _\infty }V_\infty ^2S{C_{{D_w}}} = \frac{1}{2} \times 0.41351 \times {\left( {628.971} \right)^2} \times 20 \times 0.00084 = 1374.126N\]

Mach wave is formed by pilling up of pressure disturbances when the object is flying at a speed above the speed of sound. Mach wave is due to the weak disturbances in the flow. Mach angle is the angle between the Mach wave and the direction of the movement of the object. It depends only on the Mach number. Mach angle is given by \(\mu\).

\[\mu = {\sin ^{ – 1}}\left( {\frac{1}{M}} \right)\]

Here, Mach number is \(2.2\). Therefore, Mach angle

\[\mu = {\sin ^{ – 1}}\left( {\frac{1}{{2.2}}} \right) = {27.036^\circ }\]

Since, the airfoil is flying at a low speed, incompressible flow can be considered. We can apply the Bernoulli’s equation with density as constant. From Bernoulli’s equation

\[\begin{gathered}
p + \frac{1}{2}\rho {V^2} = {p_\infty } + \frac{1}{2}\rho V_\infty ^2 \hfill \\
\Rightarrow p – {p_\infty } = \frac{1}{2}\rho \left( {V_\infty ^2 – {V^2}} \right) \hfill \\
\end{gathered} \]

\[{C_p} = \frac{{p – {p_\infty }}}{{{q_\infty }}} = \frac{{\frac{1}{2}\rho \left( {V_\infty ^2 – {V^2}} \right)}}{{\frac{1}{2}\rho V_\infty ^2}} = \frac{{V_\infty ^2 – {V^2}}}{{V_\infty ^2}} = 1 – \left( {\frac{V}{{V_\infty }}} \right)^2\]

Therefore, coefficient of pressure,

\[{C_p} = 1 – {\left( {\frac{V}{{{V_\infty }}}} \right)^2} = 1 – {\left( {\frac{{58}}{{50}}} \right)^2} = – 0.3456\]

The dynamic pressure for the airfoil is

\[{q_\infty } = \frac{1}{2}{\rho _\infty }V_\infty ^2 = \frac{1}{2} \times 1.225 \times {\left( {40} \right)^2} = 980N/{m^2}\]

Area per unit span, \(S = 1 \times (c) = 1 \times 1 = 1\)

Therefore, lift per unit span,

\[L = {q_\infty }S{c_l} = 980 \times 1 \times 0.85 = 833\,N\]

Drag per unit span,

\[D = {q_\infty }S{c_d} = 982 \times 1 \times 0.075 = 73.5\,N\]

Moment about the quarter chord per unit span,

\[{M_{c/4}} = {q_\infty }Sc{c_{{m_{c/4}}}} = 980 \times 1 \times 1 \times \left( { – 0.028} \right) = – 27.44Nm\]

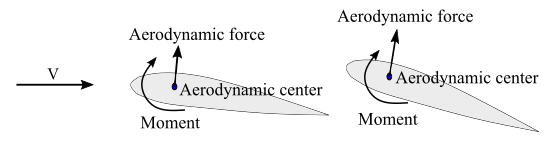
Center of pressure: When a fluid flows around the surface of an object, there is a variation of pressure on the surface, due to variation in velocity over the surface. Center of pressure is the average location of pressure on the surface of the object. Aerodynamic forces act through this center of pressure. Aerodynamic forces can be resolved into components of lift and drag. Aerodynamic moment is zero at the center of pressure.

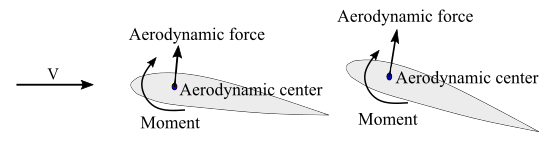Center of pressure changes with angle of attack

Aerodynamic center:  When an object is moving through air, the velocity of air varies over the surface of the object. These variation of velocity creates a variation of pressure on the surface. The pressure distribution on the object also imparts torque or moment. On changing the angle of attack, pressure distribution and thus location of center of pressure, aerodynamic forces and aerodynamic moment changes.

Aerodynamic moment can be computed at any location on the airfoil, if the location of aerodynamic forces applied is known. However, there is a point on the airfoil, where the aerodynamic moment remains constant with the change in the angle of attack. This point is called the aerodynamic center. So, if the aerodynamic forces act through the aerodynamic center, aerodynamic moment remains constant, with any angle of attack. Aerodynamic center is 1/4 chord for low speed airfoils and at nearly 1/2 chord for supersonic airfoils.

Aerodynamic center does not change with angle of attack

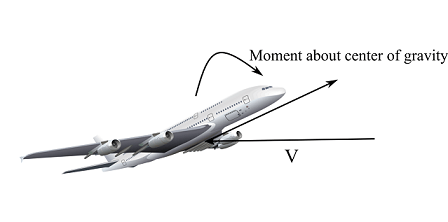
Longitudinal static stability : It is the stability of an aircraft in longitudinal or pitching flight conditions. Pitching motion of an aircraft is its nose up and down movement on the pitch axis which is also called the lateral axis, perpendicular to the aircraft’s centerline and lies in the plane of wings.

Longitudinal static stability

An airplane is flying in equilibrium when the sum of all forces and moments acting on the airplane is zero. If there is a change in the angle of attack of an aircraft  by a gust, there is a change in forces and moments and this change can produce the nose up of the airplane still further, for this case airplane will be longitudinal statically unstable and the motion of the airplane will diverge from its equilibrium.

However, if the airplane generates a restoring force and moment to bring the airplane back to equilibrium condition then the airplane has longitudinal static stability. There can be a situation when the airplane can have a tendency to maintain the disturbed position, in such a case it is in longitudinal neutral static stability.

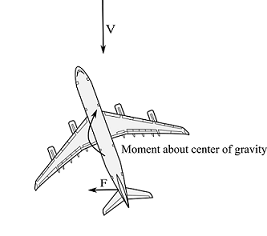
Directional static stability: It is the stability of an airplane associated with the yawing motion. Yawing motion is the airplane’s movement of nose left and right about the yaw axis which is perpendicular to the wing and lies in the airplane’s centerline plane. Fuselage and vertical stabilizer are the important components in directional stability.

Directional static stability

An airplane flying in equilibrium condition will have no yaw and the yaw angle will be zero. An airplane should generate a positive restoring yawing moment about the center of gravity if it is disturbed to a negative yaw angle. Similarly, it should generate a negative restoring yaw moment if it is disturbed to a positive yaw angle. This is directional static stability.

If the airplane has a tendency to increase its disturbed position, moving away from its equilibrium position then it has directional static unstability or is directionally unstable. If the airplane has tendency to hold its disturbed position, then the airplane has a directional neutral stability or is  neutral directional stable.

Lateral static stability: It is the rolling stability. If an aircraft when disturbed rolls to some bank angle and then generates forces and moments that will tend to reduce the bank angle and come back to equilibrium flight conditions, the airplane is said to have lateral static stability. 

Lateral static stability

Lateral stability can be achieved by the dihedral. Position of wing and wing sweep has also an effect on lateral stability. There is always a cross-coupling between the yawing and rolling motion of an airplane, so lateral and directional stability are interrelated.