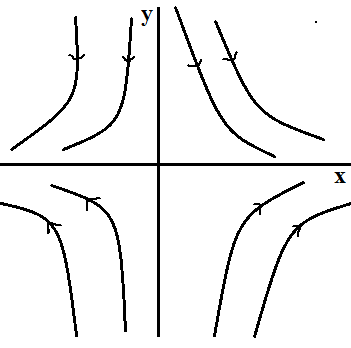
Consider a velocity field where the x and y components of velocity are given by u = cx and v = −cy, where c is a constant. Obtain the equations of the streamlines.
Consider a velocity field where the x and y components of velocity are given by u = cx and v = −cy, where c is a constant. Obtain the equations of the streamlines.
Here u=cx and v=-cy.Since vdx – udy=0
Therefore \frac{dy}{dx}=\frac{v}{u}=\frac{-y}{x} \\\Rightarrow \frac{dy}{y}=\frac{-dx}{x}
On integrating ln(y)=xln(x)+C_{1} \\\Rightarrow y=\frac{C_{2}}{x}
These streamlines are in hyperbola shape.