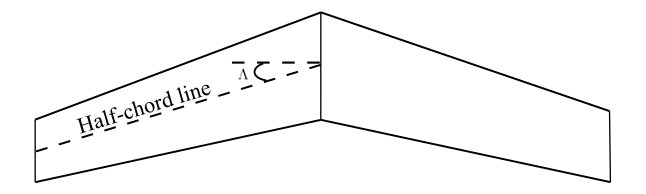
A finite wing with an elliptical lift distribution has an aspect ratio of \(6\). The airfoil of the wing has a lift slope of \(0.15\) per degree. Find and compare the lift slopes for a straight wing and a swept wing with a half-chord line sweep of \(30^{\circ}\).
A finite wing with an elliptical lift distribution has an aspect ratio of \(6\). The airfoil of the wing has a lift slope of \(0.15\) per degree. Find and compare the lift slopes for a straight wing and a swept wing with a half-chord line sweep of \(30^{\circ}\).
High aspect ratio straight wing
Using Helmbold’s equation, for calculating the lift slope for straight wing, \[a = \frac{a_{0}}{\sqrt{1+\left ( \frac{a_{0}}{\pi AR} \right )^{2}}+\left ( \frac{a_{0}}{\pi AR} \right )}\] Lift slope for the airfoil \(= a_{0} = 0.15\,/degree = 8.5944\,/radian\).
Therefore,
\[a = \frac{8.5944}{\sqrt{1+\left ( \frac{8.5944}{\pi \left ( 6 \right )} \right )^{2}}+\left ( \frac{8.5944}{\pi \left ( 6 \right )} \right )}=1.4569\,per\,radian\]
Using Helmbold’s equation, for calculating the lift slope for a swept wing ,\[a = \frac{a_{0}cos\Lambda }{\sqrt{1+\left ( \frac{a_{0}cos\Lambda}{\pi AR} \right )^{2}}+\left ( \frac{a_{0}cos\Lambda}{\pi AR} \right )}\]Here, \(\Lambda = 30^{0}\), is the sweep angle of the wing referenced to the half-chord line. Therefore, \[a = \frac{8.5944cos30^{0}}{\sqrt{1+\left ( \frac{8.5944cos30^{0}}{\pi \left ( 6 \right )} \right )^{2}}+\left ( \frac{8.5944cos30^{0}}{\pi \left ( 6 \right )} \right )}=1.4436\,per\,radian\]On comparing the lift slopes of straight wing and swept wing, we can see that there is a reduction in lift slope for the swept wing.
Wing sweep is decreasing the lift slope, and it affects lift slope to a larger degree for a high aspect ratio wings than for a lower aspect ratio wings.
