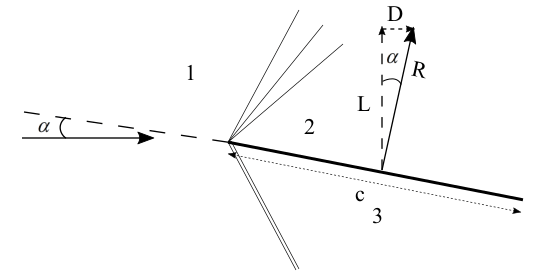Supersonic flow over a thin flat plate at an angle of attack

From the \(\theta -\beta -M\) relationship, for \(\theta = 8^{\circ}\) and \(M = 3\), \(\beta =25.611^{\circ}\)
Therefore,
\[M_{n1}=M_{1}Sin\beta =3Sin\left ( 25.611^{\circ} \right )=1.297\]
From normal shock properties, for \(M_{n1}=1.297\), \(\frac{p_{3}}{p_{1}}=1.796\)
From isentropic flow properties, for \(M_{1}=3\), \(\left ( \frac{p_{1}}{p_{01}} \right )=0.02722\)
From prandtl-Meyer function for \(M_{1}=3\), \(\nu _{1}=49.76\)
Therefore, \[\nu _{2}=\nu _{1}+\theta =49.76^{\circ}+8^{\circ}=57.76^{\circ}\]
For, \(\nu _{2}=57.76^{\circ}, M_{2}=3.452\)

For, \(M_{2}=3.452\), from isentropic flow properties
\[\left ( \frac{p_{2}}{p_{02}} \right )=0.01404\]

Therefore,
\[\frac{p_{2}}{p_{1}}=\left ( \frac{p_{2}}{p_{02}} \right )
\left ( \frac{p_{02}}{p_{01}} \right )\left ( \frac{p_{01}}{p_{1}} \right )=\left ( 0.01404 \right )
\left ( 1 \right )\left ( \frac{1}{0.02722} \right )=0.5158\]

Total pressure is constant through the expansion wave, \(p_{02}=p_{01}\).
For, a thin flat plate lift per unit span is \(L{}’=\left ( p_{3}-p_{2} \right )\left ( c \right )cos\alpha\)

also, \[c_{l}=\frac{L{}’}{q_{1}S}
=\frac{L{}’}{\frac{\gamma }{2}p_{1}M_{1}^{2}c}
=\frac{\left ( p_{3}-p_{2} \right )\left ( c \right ) cos\alpha }{\frac{\gamma }{2}p_{1}M_{1}^{2}c}
=\frac{2}{\gamma M_{1}^{2}}\left ( \frac{p_{3}}{p_{1}}-\frac{p_{2}}{p_{1}} \right )cos\alpha \]
\[\Rightarrow c_{l}=\frac{2}{\left ( 1.4 \right )\left ( 3^{2} \right )}\left ( 1.796-0.5158 \right )cos\left ( 8^{\circ} \right )=0.20123\]

For a thin flat plate, drag per unit span is \(D{}’=\left ( p_{3}-p_{2} \right )\left ( c \right )sin\alpha\)
also,
\[c_{d}=\frac{D{}’}{q_{1}S}=\frac{D{}’}{\frac{\gamma }{2}p_{1}M_{1}^{2}c}
=\frac{\left ( p_{3}-p_{2} \right )\left ( c \right ) sin\alpha }{\frac{\gamma }{2}p_{1}M_{1}^{2}c}
=\frac{2}{\gamma M_{1}^{2}}
\left ( \frac{p_{3}}{p_{1}}-\frac{p_{2}}{p_{1}} \right )sin\alpha\]
\[\Rightarrow c_{d}=\frac{2}{\left ( 1.4 \right )\left ( 3^{2} \right )}\left ( 1.796-0.5158 \right )sin\left ( 8^{\circ} \right )=0.02828\]