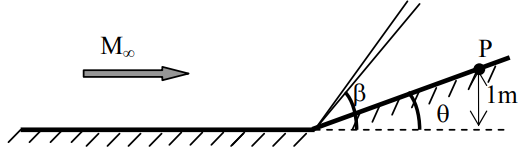
Find the shock angle and the total temperature at point P.
Consider an inviscid, adiabatic flow of air at free stream Mach number M_{\infty}=2, across a compression corner \left ( \theta =20^{\circ} \right ) as shown. The free stream total enthalpy is h_{0,\infty}=810\;kJ/kg. Assume that air is calorically perfect with \gamma=1.4,R=287\;J/kg-K.
Find the shock angle \beta and total temperature at point P.
Here an oblique shock wave is formed at the corner of the body. There are two components of incoming flow velocity, a normal flow component and a tangential flow component to the oblique shock wave. Tangential component of flow velocity is constant across the shock wave.
Normal component of flow velocity changes which must be greater than speed of sound so that oblique shock wave occur. Normal component of incoming flow velocity is u_{\infty}sin\beta and let speed of sound be a_{1}.ThereforeV_{n}sin\beta> a_{1} \\\Rightarrow \frac{V_{n}}{ a_{1}}sin\beta> 1 \\\Rightarrow M_{\infty}sin\beta>1 \\\Rightarrow \beta=sin^{-1}\left ( \frac{1}{M_{\infty}} \right ) \\\Rightarrow \beta>sin^{-1}\left ( \frac{1}{2} \right ) \\\Rightarrow \beta>30^{\circ}
Across shock wave total temperature does not changes. Therefore, total temperature at point P will be given as h=C_{p}T \\C_{p}=1004.5\;J/kg-K \\\Rightarrow T_{0,2}=T_{0,1}=\frac{h_{0,\infty}}{C_{p}}=\frac{810000}{1004.5} \\=806.37\;K