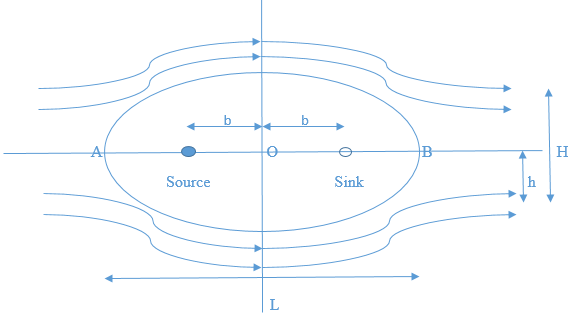
Consider the superposition of a uniform flow 29 m/s, a source of strength 50m^2/s and a sink of strength –50m^2/s. The distance between the source and sink is 2m. Find the slenderness ratio of the Rankine oval, that is the ratio of the horizontal and vertical lengths for an oval shape.
Consider the superposition of a uniform flow 29 m/s, a source of strength 50 m^2/s and a sink of strength –50 m^2/s. The distance between the source and sink is 2m. Find the slenderness ratio of the Rankine oval, that is the ratio of the horizontal and vertical lengths for an oval shape.
Slenderness ratio of the Rankine oval is L/H
L=2 OA =2 OB = \sqrt{b^{2}+\frac{\Lambda b }{\pi V_{\infty}}}
L=2\sqrt{1+\frac{50}{\pi\times29 }} \\=2.489\;m
\left ( \frac{h}{b} \right )=\frac{1}{2}\left \{ \frac{h^{2}}{b} -1\right \}tan\left \{ 2\left ( \frac{\pi V_{\infty} b}{\Lambda} \right )\frac{h}{b} \right \} \\\Rightarrow \left ( \frac{h}{1} \right )=\frac{1}{2}\left \{ \frac{h^{2}}{1}-1 \right \}tan\left \{ 2\left ( \frac{\pi V_{\infty }1}{\Lambda} \right ) \frac{h}{1}\right \} \\\Rightarrow h=\frac{1}{2}\left \{ h^{2}-1 \right \}tan\left \{ 2\left ( \frac{\pi 29}{\Lambda} \right )h \right \} \\\Rightarrow h=\frac{1}{2}\left \{ h^{2}-1 \right \}tan\left \{ \left ( \frac{\pi 58}{50} \right )h \right \} \\\Rightarrow 2h=\left ( h^{2}-1 \right )tan\left \{ \left ( 3.644 \right )h \right \}
Solving for h, h = 0.5755 = 2h = H = 1.151
Therefore slender ratio of the Rankine oval is
\frac{L}{H}=\frac{2.489}{1.151}=2.16246