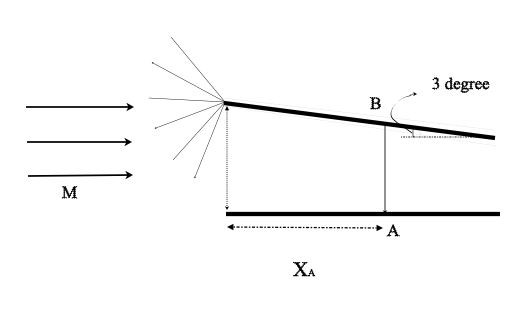
Consider a two-dimensional duct with a straight horizontal lower wall, and a straight upper wall inclined upward through the angle 3 degree. Calculate the average flow Mach number over AB, assuming that M varies linearly along that portion of AB inside the expansion wave.
Calculate the average flow Mach number over AB, assuming that M varies linearly along portion AB inside the expansion wave.The height of the duct entrance is 0.3 m . A uniform horizontal flow at Mach 2 enters the duct and goes through a Prandtl-Mayer expansion wave centered at the top corner of the entrance.The wave propagates to the bottom wall at point A located at distance {X_A} from the duct entrance.Imagine a line drawn perpendicular to the lower wall at point A, and intersecting the upper wall at point B.
We need to obtain \nu \left( {{M_2}} \right) from Prandtl-Meyer expansion function.
\theta = \nu \left( {{M_2}} \right) – \nu \left( {{M_1}} \right)
We need to calculate \nu \left( {{M_1}} \right) from Appendix C “Prandtl-Meyer expansion function and Mach angle table” for
{M_1} = 2,{\nu _1} = {26.38^ \circ }
On substituting this value
\begin{array}{l}{3^ \circ } = \nu \left( {{M_2}} \right) – \nu \left( {{M_1}} \right)\\{3^ \circ } = \nu \left( {{M_2}} \right) – {26.38^ \circ }\\\nu \left( {{M_2}} \right) = {26.38^ \circ } + {3^ \circ }\\ = {29.38^ \circ }\end{array}
We need to obtain {M_2} from Appendix C “Prandtl-Meyer expansion wave and Mach angle table”, for
\begin{array}{l}\nu \left( {{M_2}} \right) = {29.38^ \circ }\\{M_2} = 2.1\end{array}
So, average Mach number across AB is {2.1}