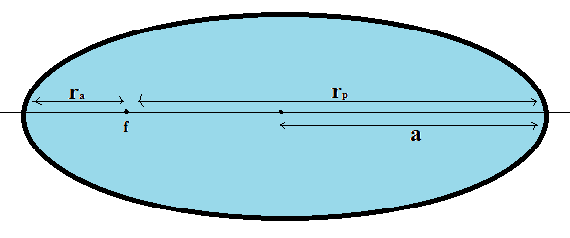
An elliptic orbit has its perigee at 400 km above the earth’s surface and apogee at 3400 km above the earth’s surface. For this orbit, what is the eccentricity and semi-major axis respectively.
An elliptic orbit has its perigee at 400 km above the earth’s surface and apogee at 3400 km above the earth’s surface. For this orbit, what is the eccentricity and semi-major axis respectively.
Let the radius of earth be 6400\;km.
r_{p} = 40\;km \\r_{a} = 3400\;km
r_{p}=a(1-e) \\r_{a}=a(1+e)
On putting the values and on adding we get
a(1-e)=40+6400=6800\;km \\a(1+e)=3400+6400=9800\;km \\\Rightarrow 2a=16600\;km \\\Rightarrow a=8300\;km
Therefore semi major axis a = 8300\;km.On substituting the value of ‘a’ in one of the above equation we get
8300(1+e)=9800\;km
\Rightarrow e=0.18
Therefore eccentricity e = 0.18