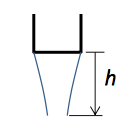
A smooth, steady stream of liquid (density, rho;) emanates downward from a circular faucet (to the atmosphere). The exit area of the faucet is A1. The volumetric flow rate is Q. Find the weight of the given section of the fluid stream.
A smooth, steady stream of liquid (density, rho;) emanates downward from a circular faucet (to the atmosphere). The exit area of the faucet is A1. The volumetric flow rate is Q.
Find the weight of the given section of the fluid stream (between the faucet exit and distance h)
Ignore the following: drag, buoyancy, effects of surface tension. Assume the following: the radial contribution to fluid velocity is negligible (except in the sense that it explains the narrowing of the stream); and the pressure within the stream is zero (gage).
Velocity at the exit of the faucet
V_{1}=\frac{Q}{A}
On applying Bernoulli principle between the faucet and the flow at h, the velocity of flow at height h is
\frac{P_{1}}{\rho g}+\frac{V_{1}^{2}}{2g}+Z_{1}=\frac{P_{2}}{\rho g}+\frac{V_{2}^{2}}{2g}+Z_{2} \\\Rightarrow \frac{V_{1}^{2}}{2g}+Z_{1}=\frac{V_{2}^{2}}{2g}+Z_{2} \\\Rightarrow z_{1}-z_{2}=\frac{V_{1}^{2}-V_{2}^{2}}{2g} \\\Rightarrow h=\frac{V_{1}^{2}-V_{2}^{2}}{2g} \\\Rightarrow V_{2}=\sqrt{V_{1}^{2}-2gh}
Area of flow at height h will be
A_{2}=\frac{Q}{V_{2}} \\=\frac{Q}{\sqrt{V_{1}^{2}-2gh}} \\=\frac{Q}{\sqrt{\left (\frac{Q}{A_{1}} \right )^{2}-2gh}}
The flow from the faucet to the height h is shape like of frustum of a cone.Therefore weight of the water will be given as
\\W=mg \\=\rho Vg \\=\rho \left ( \frac{\pi h}{3}\left ( R^{2}+Rr+r^{2} \right ) \right )g \\=\rho \left ( \frac{\pi h}{3}\left ( \frac{A_{1}}{\pi}+\left ( \sqrt{\frac{A_{1}}{\pi }}\times\sqrt{\frac{Q}{\frac{\sqrt{\left ( \frac{Q}{A_{1}} \right )^{2}-2gh}}{\pi}}} \right )+\frac{Q}{\frac{\sqrt{\left ( \frac{Q}{A_{1}} \right )^{2}-2gh}}{\pi}} \right ) \right )g