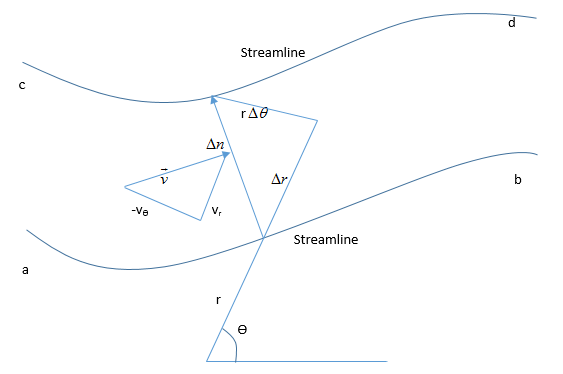
Consider a flow field in polar coordinates, where the stream function is given as \(ψ = ψ(r, θ)\). Starting with the concept of mass flow between two streamlines, derive Equations \(\rho V_{r}=\frac{1}{r}\frac{\partial \bar{\psi }}{\partial \theta}\) and \(\rho V_{\theta}=-\frac{\partial\bar{\psi} }{\partial r}\).
Consider a flow field in polar coordinates, where the stream function is given as \(ψ = ψ(r, θ)\). Starting with the concept of mass flow between two streamlines, derive Equations \[\rho V_{r}=\frac{1}{r}\frac{\partial \bar{\psi }}{\partial \theta}
\\\rho V_{\theta}=-\frac{\partial\bar{\psi} }{\partial r}\]
\(\psi =\psi\left ( r,\theta \right )\)
Mass flow between streamlines =\(\Delta \bar {\psi}\) \[\Delta \bar{\psi}=\rho V \Delta n
\\\Delta \bar {\psi} = \left ( -\rho V_{\theta} \right ) \Delta r+\rho V_{r}\left ( r\theta \right )\]
Let ‘cd’ approaches ‘ab’:
\[d\bar{\psi}=-\rho V_{\theta}dr+\rho rV_{r}d\theta\]
Also, since \(\bar{\psi}=\bar{\psi}\left ( r,\theta \right )\),from calculus \[d\bar{\psi}=\frac{\partial \bar{\psi}}{\partial r}dr+\frac{\partial \bar{\psi}}{\partial \theta}d\theta\]
On comparing \[-\rho V_{\theta}=\frac{\partial \bar{\psi}}{\partial r}\] and \[\rho r V_{r}=\frac{\partial \bar{\psi }}{\partial \theta} \]
or \[\rho V_{r}=\frac{1}{r}\frac{\partial \bar{\psi}}{\partial \theta}\] and \[\rho V_{\theta}=-\frac{\partial\bar{\psi} }{\partial r}\]