Consider an incompressible two-dimensional viscous flow over a curved surface. Let the pressure distribution on the surface be p(s)=2+sin\left ( \frac{\pi}{2}+s \right )\;N/m^2,where s is the distance along the curved surface from the leading edge. Find the distance from where the flow separates.
Consider an incompressible two-dimensional viscous flow over a curved surface. Let the pressure distribution on the surface be p(s)=2+sin\left ( \frac{\pi}{2}+s \right )\;N/m^2,where s is the distance along the curved surface from the leading edge. Find the distance from where the flow separates.
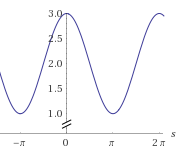
p\left ( s \right )=2+sin\left ( \frac{\pi}{2}+s \right )
The graph of the above function is
From the graph we easily see that at s = \pi there will be adverse pressure gradient.So the separation will start from this point.