Find the pressure, temperature , Mach number, total pressure and total temperature behind the oblique shock wave.
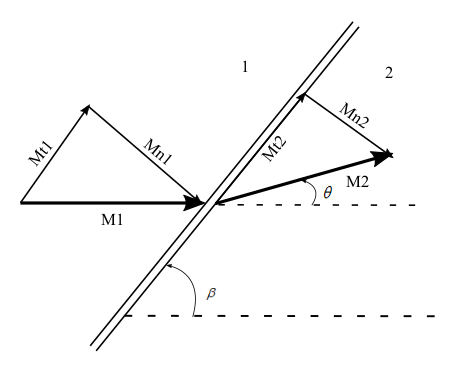
An oblique shock wave is generated with a wave angle of {30^ \circ } in a Mach 4 flow, at an altitude of 9000\,m. Find the pressure, temperature , Mach number, total pressure and total temperature behind the oblique shock wave.
Normal component of the upstream Mach number to the oblique shock wave,
M_{n1}=M_{1}Sin\beta =4\left ( Sin30^{\circ} \right )=2
From Normal shock wave properties table, for M_{n1}=2
\frac{p_{2}}{p_{1}}=4.5, \frac{T_{2}}{T_{1}}=1.687, \frac{p_{02}}{p_{01}}=0.7209, M_{n2}=0.5774
At an altitude of 9000\, m , p_{1}=3.08\times 10^{4} N/m^{2} , T_{1}=229.74K
Therefore,
P_{2}=\left ( \frac{P_{2}}{P_{1}} \right )P_{1}=\left ( 4.5 \right )\left ( 3.08\times 10^{4} \right)= 13.86\times 10^{4} N/m^{2}
T_{2}=\left ( \frac{T_{2}}{T_{1}} \right )T_{1}=\left ( 1.687 \right )229.74=387.571K
From the \theta -\beta -M diagram , for, wave angle of \beta =30^{\circ} and Mach number of 4, deflection angle, \theta =17.7^{\circ}.
Therefore,
M_{2}=\frac{M_{n2}}{Sin\left ( \beta -\theta \right )}=\frac{0.5774}{Sin\left ( 30^{\circ} -17.7^{\circ}\right )}=2.710
From the table of isentropic flow properties , for
M_{1}=4,\frac{p_{01}}{p_{1}}=151.8,\frac{T_{01}}{T_{1}}=4.2
Total pressure,
p_{02}=\left ( \frac{p_{02}}{p_{01}} \right )\left ( \frac{p_{01}}{p_{1}} \right )p_{1}=\left ( 0.0709 \right )\left ( 151.8 \right )\left ( 3.08\times 10^{4} \right )=331488.696N/m^{2}
Total temperature,
T_{02}=T_{01}=\left ( \frac{T_{01}}{T_{1}} \right )T_{1}=4.2\times 229.74K=964.908K