A supersonic wind tunnel produces supersonic speeds in the test section. It consists of a nozzle, test section and a diffuser. Nozzle is convergent-divergent in design. It supplies a uniform supersonic flow into the test section which is a constant area duct. Diffuser which is also convergent-divergent slows the supersonic flow to subsonic.

A high-pressure reservoir is placed at the inlet of the nozzle to run the wind tunnel. A vacuum storage tank at the exit of the diffuser or a combination of both the high-pressure reservoir and a vacuum storage tank can also be used to run the supersonic wind tunnel.

From isentropic flow properties, for \(\frac{A_{e}}{A^{*}}=4.441\), \(M_{e}=3.05\)

From normal shock properties, for \(M_{e}=3.05\), \(\frac{p_{02}}{p_{01}}=0.3145\)

Therefore,
\[p_{01}=\left ( \frac{p_{01}}{p_{02}} \right )
p_{02}=\left ( \frac{1}{0.3145} \right )\left ( 1.5 \right )=4.7695\,atm\]

From the table of normal shock properties; for, Mach number of \(2.8\), \(\frac{{{p_2}}}{{{p_1}}} = 8.98\), \(\frac{{{\rho _2}}}{{{\rho _1}}} = 3.664\), \(\frac{{{T_2}}}{{{T_1}}} = 2.451\), \(\frac{{{p_{02}}}}{{{p_1}}} = 10.57\), \({M_2} = 0.4882\).

Therefore,

\[{p_2} = 8.98{p_1} = 8.98\left( {1atm} \right) = 8.98\,atm\]

\[{T_2} = 2.451{T_1} = 2.451\left( {295} \right) = 723.045\,K\]

\[{p_{_1}} = {\rho _1}R{T_1} \Rightarrow {\rho _1} = \left( {\frac{{1 \times \left( {1.01 \times {{10}^5}} \right)}}{{287 \times 295}}} \right) = 1.193\,kg/{m^3}\]

\[{\rho _2} = 3.664\left( {1.193} \right) = 4.371\,kg/{m^3}\]

\[{p_{02}} = \left( {\frac{{{p_{02}}}}{{{p_1}}}} \right){p_1} = 10.57\left( 1 \right) = 10.57\,atm\]

From isentropic flow properties table, for, Mach number of  \(2.8\),  \[\frac{{{T_{01}}}}{{{T_1}}} = 2.568\]

Since, \({T_{02}} = {T_{01}}\), Total temperature is constant,

Therefore,

\[{T_{02}} = \left( {\frac{{{T_{01}}}}{{{T_1}}}} \right){T_1} = 2.568 \times \left( {295} \right) = 757.56\,K\]

 

Speed of sound is given by \[a = \sqrt {\gamma RT} \]

Speed of sound depends on the type of the medium and its temperature. In air it depends on  the type of the gas and its temperature. On Earth, atmosphere is composed of mostly nitrogen and oxygen and temperature varies with the altitude.

\[a = \sqrt {1.4 \times 287 \times 250} = 316.94\,m/s\]

Mars has an atmosphere which is composed mostly of carbon dioxide.

Burnout velocity: It is the velocity of a rocket at the instant of burnout of its propellant. There is a depletion of propellants. Burnout velocity is given as

\[{V_b} = {g_0}{I_{sp}}\ln \left( {\frac{{{M_i}}}{{{M_f}}}} \right)\]

Burnout velocity for the first stage is

\[{V_{b1}} = {g_0}{I_{sp}}\ln \left( {\frac{{{M_L} + {M_{s1}} + {M_{s2}} + {M_{p1}} + {M_{p2}}}}{{{M_L} + {M_{s1}} + {M_{s2}} + {M_{p2}}}}} \right)\]

\[ \Rightarrow {V_{b1}} = \left( {9.8} \right)\left( {290} \right)\ln \left( {\frac{{100 + 900 + 700 + 8000 + 6000}}{{100 + 900 + 700 + 6000}}} \right) = 2024.76\,m/s\]

Increase in velocity with the second stage is,

\[{V_{b2}} – {V_{b1}} = {g_0}{I_{sp}}\ln \left( {\frac{{{M_L} + {M_{s2}} + {M_{p2}}}}{{{M_L} + {M_{s2}}}}} \right)\]

\[ \Rightarrow {V_{b2}} – {V_{b1}} = \left( {9.8} \right)\left( {290} \right)\ln \left( {\frac{{100 + 700 + 6000}}{{100 + 700}}} \right) = 6082.07\,m/s\]

Therefore,

\[{V_{b2}} – {V_{b1}} = 6082.07 \Rightarrow {V_{b2}} = 6082.07 + 2024.76 = 8106.83\,m/s\]

Thrust produced by the engine is

\[T = \dot m\left( {{V_e} – {V_\infty }} \right) + \left( {{P_e} – {P_\infty }} \right){A_e}\]

\[ \Rightarrow 5000 = \dot m\left( {650 – 300} \right) + \left( {104000 – 101325} \right)0.08\]

\[ \Rightarrow \dot m = 13.7\,kg/s\]

and,

\[\dot m = {\rho _\infty }{V_\infty }{A_i}\]

\[ \Rightarrow {13.7} = 1.225 \times 300 \times {A_i}\]

\[ \Rightarrow {A_i} = \frac{{13.7}}{{367.5}} = 0.037{m^2}\]

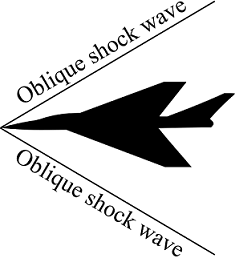
Shock waves are very thin regions across which the fluid properties change significantly. Shock waves are created when the object travels beyond the speed of sound. Any object traveling in the atmosphere creates pressure disturbances. When the object travels beyond the speed of sound it creates a stronger pressure disturbance. These pressure disturbances pile up and merge to form a shock wave.
Shock waves are oblique shock waves, normal shock waves, bow shock waves, and expansion waves. Oblique shock waves are oblique to the flow direction. Oblique shock waves are created by a sharp nose body, like a wedge. Normal shock is normal or perpendicular to the flow direction. A normal shock wave occurs in front of a detached shock wave.

Oblique shock wave

A shock wave which is detached from the object is a bow shock wave. A bow shock wave is created by a blunt body. Bow shock waves are curved.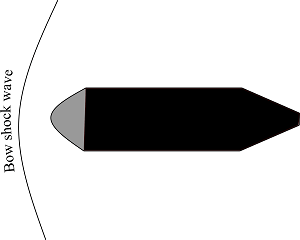

Bow shock wave around a blunt body

Expansion waves are formed when supersonic flow turns over a convex corner. Expansion wave consists of an infinite number of Mach waves.

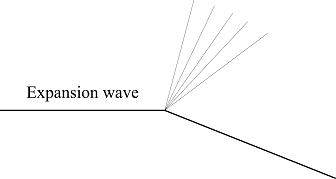Expansion wave at a convex corner

Across a normal and oblique shock wave pressure, density, temperature increases, and Mach number decreases. Across an expansion wave pressure, temperature, density decreases, and Mach number increases.

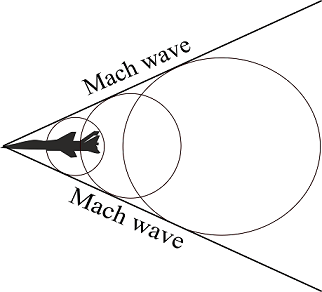
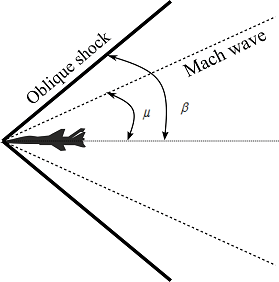
An object moving in the atmosphere creates pressure disturbances. If the object is traveling less than the speed of sound, the object lies inside the pressure disturbances. If the object is moving more than the speed of sound, the object is outside of the pressure disturbances. Here, these pressure disturbances pile up behind the object. A tangent line over the piled pressure disturbances forms the Mach wave.

Origin of Mach wave

Mach wave makes an angle with the direction of the movement of the object called the Mach angle. Mach angle is the sine inverse of the Mach number. That is

\[Mach\,angle = {\sin ^{ – 1}}\left( {\frac{1}{M}} \right)\]

If the pressure disturbances created by the moving object are stronger than the sound wave, it will make a shock wave. Mach wave is the limiting case of an oblique shock wave.

Oblique shock wave

We need to calculate the Mach number of the flow. Speed of sound,

\[{a_\infty } = \sqrt {\gamma R{T_\infty }} = \sqrt {1.4 \times 287 \times 285} = 338.398\,m/s\]

Therefore, Mach number of the flow is

\[{M_\infty } = \frac{{{V_\infty }}}{{{a_\infty }}} = \frac{{235}}{{338.398}} = 0.694\]

Mach number of \(0.694\) shows that the flow is compressible. Density of flow is obtained on applying the equation of state.

\[{p_\infty } = {\rho _\infty }R{T_\infty } \Rightarrow {\rho _\infty } = \frac{{{p_\infty }}}{{R{T_\infty }}} = \frac{{1.01 \times {{10}^5}}}{{287 \times 285}} = 1.235\,kg/{m^3}\]

Temperature at the point on the wing can be calculated from the energy equation,

\[{C_p}T + \frac{{{V^2}}}{2} = {C_p}{T_\infty } + \frac{{V_\infty ^2}}{2}\]

\(C_p\) for air is

\[{C_p} = \frac{{\gamma R}}{{\gamma – 1}} = \frac{{1.4 \times 287}}{{1.4 – 1}} = 1004.5\,kJ/kg.K\]

Therefore,

\[\left( {1004.5 \times T} \right) + \frac{{{{\left( {251} \right)}^2}}}{2} = \left( {1004.5 \times 285} \right) + \frac{{{{\left( {235} \right)}^2}}}{2}\]

\[ \Rightarrow 1004.5T + \frac{{{{\left( {251} \right)}^2}}}{2} = 286282.5 + \frac{{{{\left( {235} \right)}^2}}}{2}\]

\[ \Rightarrow 1004.5T = 286282.5 + \frac{{\left( {{{235}^2} – {{251}^2}} \right)}}{2}\]

\[ \Rightarrow T = 281.129\,K\]

Pressure at the point will be calculated as

\[\frac{p}{{{p_\infty }}} = {\left( {\frac{T}{{{T_\infty }}}} \right)^{\frac{\gamma }{{\gamma – 1}}}}\]

\[ \Rightarrow p = 1.01 \times {10^5}{\left( {\frac{{281.129}}{{285}}} \right)^{\frac{{1.4}}{{1.4 – 1}}}} = 96279.568\,N/{m^2}\]

Therefore, coefficient of pressure at the point will be,

\[{C_p} = \frac{{p – {p_\infty }}}{{{q_\infty }}} = \frac{{96279.568 – 1.01 \times {{10}^5}}}{{\frac{1}{2} \times 1.235 \times {{\left( {235} \right)}^2}}} = \, – 0.1384\]

When the velocity of flow is reduced to \(34\,m/s\), It is a low speed flow. Therefore, pressure coefficient at the same point can be calculated from Prandtl-Glauert rule,

\[{C_p} = \frac{{{C_{p0}}}}{{\sqrt {1 – M_\infty ^2} }} \Rightarrow\, – 0.1384 = \frac{{{C_{p0}}}}{{\sqrt {1 – {{\left( {0.694} \right)}^2}} }} \Rightarrow {C_{p0}} = \,-0.099644\]

 

Pressure coefficient is given as

\[{C_p} = \frac{{p\, – \,{p_\infty }}}{{{q_\infty }}}\]

Dynamic pressure,

\[{q_\infty } = \frac{1}{2}{\rho _\infty }V_\infty ^2 = \frac{1}{2} \times 1.225 \times {\left( {40} \right)^2} = 980\]

Therefore, \(C_p\) is

\[{C_p} = \frac{{0.89 \times {{10}^5} \,-\, 1.01 \times {{10}^5}}}{{980}} =\, – 12.24\]

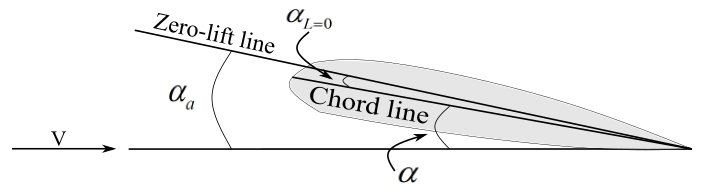
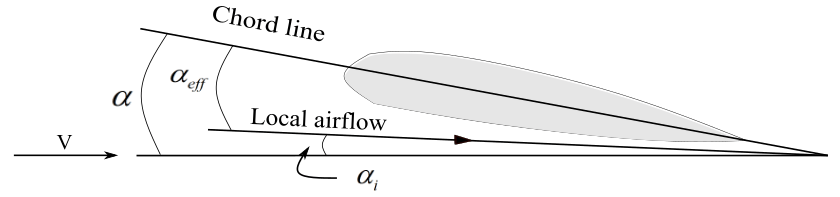
Angle of attack: For an airfoil, it is the angle between the chord line and the direction of the relative wind. In general, angle of attack is the angle between a reference line on the airplane or wing and the relative wind. The reference line can be a chord line in case of an airfoil, a line from leading edge to trailing edge at some average point on wing, or a centerline of a fuselage.

Reference line does not make any difference if it is used consistently. An increase in angle of attack increases the coefficient of lift up to a point. This point is called the critical angle of attack. If the angle of attack is increased beyond this critical angle, stall takes place and there is a decrease in coefficient of lift.

Absolute angle of attack: It is the angle between the zero-lift line and the relative wind. Zero-lift line is a line through an airfoil when zero lift is produced. The zero-lift line is drawn from the trailing edge and is parallel to the relative wind. The airfoil is at zero-lift angle of attack. Zero-lift line is symmetric with chord for a symmetrical airfoil. For a cambered airfoil, the zero-lift line lies above the chord line, as the zero-lift angle of attack is negative for such airfoils. Absolute angle of attack is the sum of the angle of attack and angle of attack at zero-lift. If the absolute angle of attack is zero, then the lift is zero, for any cambered airfoil.

Absolute angle of attack

Induced angle of attack: Induced angle of attack is associated with the induced drag. Induced drag is due to trailing edge vortex, which creates downwash. Downwash deflects the free-stream air downward, in the vicinity of the wing. This deflection is the ‘induced angle’ and it is the difference between the local airflow direction of the wing and free-stream airflow direction. So, at the vicinity of the wing, an airfoil sees an effective angle of attack which is less than the angle of attack seen through the naked eye, \(\alpha _{eff} = \alpha \ -\ {\alpha _i}\).

Induced angle of attack