Pressure is defined as force per unit area. In fluid pressure on a surface is the normal force acting per unit area due to time rate of change of momentum of the gas molecules which is impacting the surface.

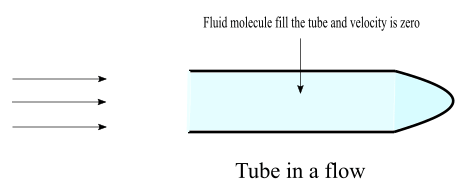
The pressure due to the pure random motion of the molecules of the gas is the static pressure. Whenever a body is in a flow, the fluid will get an obstruction at the surface of the body and the velocity of the gas molecule will be zero. If a body is a tube with one end closed, the fluid molecules will fill the tube and its velocity will be zero, that the fluid will stagnate.

A tube in a fluid flow

At the opening of the tube the fluid molecules sees obstruction. Therefore upcoming fluid molecules slows down and reduces to zero velocity. Any point in a fluid flow where flow velocity is zero is called the stagnation point. As velocity is decreased so pressure is increased. Therefore, pressure at stagnation point is larger than the static pressure.

The pressure at the stagnation point is called the stagnation pressure or total pressure.

Therefore, there are two types of pressure in a fluid flow, static pressure and total or stagnation pressure. Static pressure is the pressure which is felt when a fluid has a velocity and stagnation pressure is the pressure that is felt when flow velocity is reduced to zero.

If a flow is isentropic in between two points then the total pressure is constant at that points. An isentropic process is a process in which entropy remains constant. An isentropic process is both reversible and adiabatic.

The temperature of a gas is directly proportional to the average kinetic energy of the gas molecules. Therefore, a gas which has a high temperature, the molecules are moving randomly at a very high speed. A gas in low-temperature, there is a slow random motion of the molecules as compared to the high temperature gas.

The temperature of a fluid element when it is bought to rest adiabatically is called the total temperature. Stagnation temperature is the temperature when a moving flow is isentropically brought to rest. At the stagnation point total temperature and stagnation temperature have the same value.

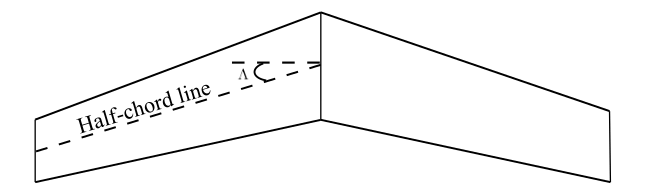
High aspect ratio straight wing

Using Helmbold’s equation, for calculating the lift slope for straight wing, $$a = \frac{a_{0}}{\sqrt{1+\left ( \frac{a_{0}}{\pi AR} \right )^{2}}+\left ( \frac{a_{0}}{\pi AR} \right )}$$ Lift slope for the airfoil $= a_{0} = 0.15\,/degree = 8.5944\,/radian$.

Therefore,

$$a = \frac{8.5944}{\sqrt{1+\left ( \frac{8.5944}{\pi \left ( 6 \right )} \right )^{2}}+\left ( \frac{8.5944}{\pi \left ( 6 \right )} \right )}=1.4569\,per\,radian$$

Swept wing

Using Helmbold’s equation, for calculating the lift slope for a swept wing , $$a = \frac{a_{0}cos\Lambda }{\sqrt{1+\left ( \frac{a_{0}cos\Lambda}{\pi AR} \right )^{2}}+\left ( \frac{a_{0}cos\Lambda}{\pi AR} \right )}$$ Here, $\Lambda = 30^{0}$, is the sweep angle of the wing referenced to the half-chord line.  Therefore,  $$a = \frac{8.5944cos30^{0}}{\sqrt{1+\left ( \frac{8.5944cos30^{0}}{\pi \left ( 6 \right )} \right )^{2}}+\left ( \frac{8.5944cos30^{0}}{\pi \left ( 6 \right )} \right )}=1.4436\,per\,radian$$ On comparing the lift slopes of straight wing and swept wing, we can see that there is a reduction in  lift slope for the swept wing.

Wing sweep is decreasing the lift slope, and it affects lift slope to a larger degree for a high aspect ratio wings than for a lower aspect ratio wings.

Span is the wingspan of the airplane. It is the distance from one wing tip to other. It is measured in a straight line and is independent of the wing shape and sweep.  Lift per unit span produced by a wing is given as ${L}’ = \frac{1}{2} \rho _{\infty}V_{\infty}^{2} c\left ( 1 \right )c_{l}$. Here, $\frac{1}{2} \rho_{\infty}V_{\infty}^{2}$ is called the dynamic pressure , $q_{\infty}$.  Coffeicent of lift, $c_{l}$, for this airfoil will be $$c_{l} = \frac{{L}’}{q_{\infty}c\left ( 1 \right )}$$ $$\Rightarrow c_{l} = \frac{1400}{\left (\frac{1}{2} \times 1.225 \times 70^{2} \right )\left ( 2.3 \right )\left ( 1 \right )}$$ $$\Rightarrow c_{l} = 0.203$$ Therefore, coefficient of lift for this airfoil is $0.203$. For, NACA $0012$ airfoil from the lift curve -slope for this airfoil, the angle of attack is $2^{\circ}$.

Pressure coefficient is given as $$C_{p}=\frac{p_{1} – p_{\infty }}{q_{\infty }}$$ This is used for incompressible to compressible flow. However, for incompressible flow, this expression can be used in terms of velocity alone, on applying the Bernoulli’s equation. On using Bernoulli’s equation for two points in a flow, $$p_{1}+\frac{1}{2}\rho V_{1}^{2} = p_{\infty } + \frac{1}{2}\rho v_{\infty }^{2}$$ $$p_{1}-p_{\infty} = \frac{1}{2} \rho \left ( V_{\infty}^{2}-V_{1}^{2} \right )$$ Considering $p_{1}$ as the pressure at a point on the wing of the aircraft, and $p_{\infty}$ as freestream pressure, coefficient of pressure is, $$C_{p} = \frac{p_{1} – p_{\infty }}{q_{\infty}}=\frac{\frac{1}{2}\rho \left ( V_{\infty}^{2}-V_{1}^{2} \right )}{\frac{1}{2}\rho V_{\infty}^{2}}=1-\left ( \frac{V_{1}}{V_{\infty}} \right )^{2}$$ $$\Rightarrow C_{p} = 1 – \left ( \frac{140}{100} \right )^{2}=-0.96$$

Velocity components are $u=\left ( 6x^{2}y+t \right )$; $v=\left ( 3yx+t^{2}+3 \right )$; $w=\left ( 3+3t^{2}y \right)$
Velocity vector is given as,
$$\vec{V}=u\hat{i}+v\hat{j}+w\hat{k}$$ At point ($3,2,4)$ and at $t=5$, velocity components will be,
$$u=\left ( 6x^{2}y+t \right )=\left ( 6\left ( 3 \right )^{2}2+5 \right )=113$$ $$v=\left ( 3yx+t^{2}+3 \right )=\left ( \left ( 3\times 2\times 3 \right )+25+3 \right )=\left ( 18+25+3 \right )=46$$ $$w=\left ( 3+3t^{2}y \right )=\left ( 3+\left ( 3\left ( 5 \right )^{2}2 \right ) \right )=\left ( 3+150 \right )=153$$
Therefore, velocity vector is,
$$\vec{V}=113\hat{i}+46\hat{j}+153\hat{k}$$ Velocity magnitude is, $$V=\sqrt{u^{2}+v^{2}+w^{2}}$$ $$=\sqrt{113^{2}+46^{2}+153^{2}}=195.69\,m/s$$

The stream function for the flow field is $$\psi =2x^{2}-y^{2}$$ Velocity component $u$ and $v$ of the two-dimensional flow field is $$u=\frac{\partial \psi }{\partial y},v=-\frac{\partial \psi }{\partial x}$$ Therefore, $$u=\frac{\partial \psi }{\partial y}=\frac{\partial }{\partial y}\left ( 2x^{2}-y^{2} \right ) =\frac{\partial }{\partial y}\left ( 2x^{2} \right )-\frac{\partial }{\partial y}\left ( y^{2} \right )=0-2y=-2y$$ $$v=-\frac{\partial \psi }{\partial x} =-\frac{\partial }{\partial x}\left ( 2x^{2}-y^{2} \right ) =-\frac{\partial }{\partial x}\left ( 2x^{2} \right )+\frac{\partial }{\partial x}\left ( y^{2} \right )=-4x+0=-4x$$ Therefore, at point $(2,3)$, $$u=-2y=-2\left ( 3 \right )=-6\\v=-4x=-4\left ( 2 \right )=-8$$ Velocity, $V=-6i-8j$
Magnitude of velocity = $$\sqrt{u^{2}+v^{2}}=\sqrt{\left ( -6 \right )^{2}+\left ( -8\right)^{2}}=\sqrt{36+64}=10$$

Flow passing through a shock wave

Specific heat at constant pressure,
$$c_{p}=\frac{\gamma R}{\gamma -1}=\frac{\left ( 1.4 \right )\left ( 287 \right )}{\left ( 1.4-1 \right )}=1004.5\,J/\left  (kg.K \right )$$
Specific heat at condtant volume,
$$c_{v}=\frac{R}{\gamma -1}=\frac{287}{0.4}=717.5\,J/kg.K$$
Enthalpy change across the shock wave,
$$h_{2}-h_{1}=c_{p}\left ( T_{2}-T_{1} \right )=1004.5\left ( 700-300 \right )=4.018\times 10^{5}\,J/kg$$
Internal energy change across the shock wave,
$$e_{2}-e_{1}=c_{v}\left ( T_{2}-T_{1} \right )=717.5\left ( 700-300 \right )=2.87\times 10^{5}\,J/kg$$
Entopy change across the shock wave,
$$s_{2}-s_{1}=c_{p}ln\left ( \frac{T_{2}}{T_{1}} \right ) -Rln\left ( \frac{p_{2}}{p_{1}} \right )=1004.5ln\left ( \frac{700}{300} \right )-287ln\left ( \frac{9}{1} \right )=220.51\,J/kg.K$$

Prandtl-Meyer expansion waves

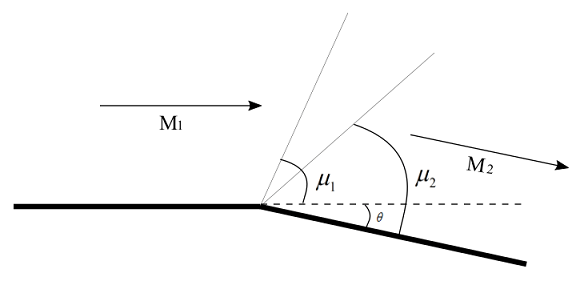
Downstream Mach number can be calculated from Prandtl-Meyer function
$$\nu (M)=\sqrt{\frac{\gamma +1}{\gamma -1}}tan^{-1}\sqrt{\frac{\gamma -1}{\gamma +1}\left ( M^{2}-1 \right )}-tan^{-1}\sqrt{M^{2}-1}$$

For a Mach number of $2.2$, $\nu \left ( M_{1} \right )=31.73^{^{\circ}}$

$$\theta =\nu \left ( M_{2} \right )-\nu \left ( M_{1} \right )$$

$$\Rightarrow \nu \left ( M_{2} \right )=\theta + \nu \left ( M_{1} \right ) = 25^{\circ}+31.73^{\circ}=56.73^{\circ}$$

for, $\nu \left ( M_{2} \right )=56.73^{^{\circ}}$, Mach number $M_{2}=3.389$

From Isentropic flow properties for, $M_{1}=2.2$

$$\frac{p_{01}}{p_{1}}=10.69$$ and
$$\frac{T_{01}}{T_{1}}=1.968$$

For, $M_{2}=3.389$
$$\frac{p_{02}}{p_{2}}=65.0798$$ and
$$\frac{T_{02}}{T_{2}}=3.297$$

Total pressure and total temperature is constant through the expansion wave, so

$p_{01}=p_{02}$ and $T_{01}=T_{02}$

Therefore,
$$p_{2}=\left ( \frac{p_{2}}{p_{02}} \right )\left ( \frac{p_{01}}{p_{1}} \right )p_{1}=\left ( \frac{1}{65.0798} \right )\left ( 10.69 \right )0.8=0.1314\,atm$$

$$T_{2}=\left ( \frac{T_{2}}{T_{02}} \right )\left ( \frac{T_{01}}{T_{1}} \right )T_{1}=\left ( \frac{1}{3.297} \right )\left ( 1.968 \right )360=214.886\,K$$

$$p_{2}=\rho _{2}RT_{2}$$

$$\Rightarrow 0.1314=\rho _{2}\left ( 287 \right )\left ( 214.886\,K \right )$$

$$\Rightarrow \rho _{2}=\frac{0.1314}{\left ( 287 \right )\left ( 214.886 \right )}=2.13\times 10^{-6}\,kg/m^{3}$$

Since,
$$p_{01}=p_{02}\Rightarrow p_{02}=\left ( \frac{p_{01}}{p_{1}} \right )\left ( p_{1} \right )=\left ( 10.69 \right )\left ( 0.8 \right )=8.552\,atm$$

Also,

$$T_{01}=T_{02}\Rightarrow T_{02}=\left ( \frac{T_{01}}{T_{1}} \right )\left ( T_{1} \right )=\left ( 1.968 \right )\left ( 360 \right )=708.48\,K$$

Mach angle is given by $\mu = Sin^{-1}\left ( \frac{1}{M} \right )$

Therefore Mach angle $\mu _{1}$ made by upstream Mach wave for $M_{1}=2.2$ is $27.04^{\circ}$

Mach angle $\mu _{2}$ made by downstream Mach wave for$M_{2}=3.389$ is $17.16^{\circ}$

and, angle made by forward Machline is $27.04^{\circ}$ and angle made by the rearward Machline is $17.16^{\circ}-25^{\circ}=-7.84^{\circ}$

Oblique shock wave

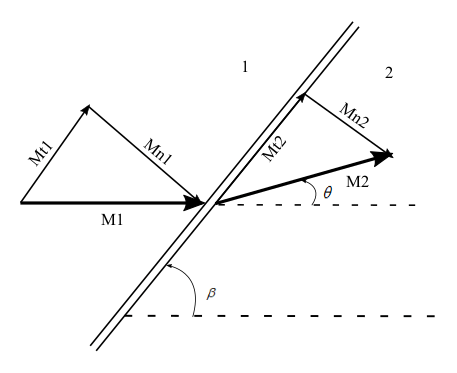
Normal component of the upstream Mach number to the oblique shock wave,

$$M_{n1}=M_{1}Sin\beta =4\left ( Sin30^{\circ} \right )=2$$

From Normal shock wave properties table, for $M_{n1}=2$

$\frac{p_{2}}{p_{1}}=4.5$, $\frac{T_{2}}{T_{1}}=1.687$,  $\frac{p_{02}}{p_{01}}=0.7209$, $M_{n2}=0.5774$

At an altitude of $9000\, m$ , $p_{1}=3.08\times 10^{4} N/m^{2}$, $T_{1}=229.74K$

Therefore,

$$P_{2}=\left ( \frac{P_{2}}{P_{1}} \right )P_{1}=\left ( 4.5 \right )\left ( 3.08\times 10^{4} \right)= 13.86\times 10^{4} N/m^{2}$$

$$T_{2}=\left ( \frac{T_{2}}{T_{1}} \right )T_{1}=\left ( 1.687 \right )229.74=387.571K$$

From the $\theta -\beta -M$ diagram , for, wave angle of $\beta =30^{\circ}$ and Mach number of $4$, deflection angle, $\theta =17.7^{\circ}$.

Therefore,

$$M_{2}=\frac{M_{n2}}{Sin\left ( \beta -\theta \right )}=\frac{0.5774}{Sin\left ( 30^{\circ} -17.7^{\circ}\right )}=2.710$$

From the table of isentropic flow properties , for

$$M_{1}=4,\frac{p_{01}}{p_{1}}=151.8,\frac{T_{01}}{T_{1}}=4.2$$

Total pressure,

$$p_{02}=\left ( \frac{p_{02}}{p_{01}} \right )\left ( \frac{p_{01}}{p_{1}} \right )p_{1}=\left ( 0.0709 \right )\left ( 151.8 \right )\left ( 3.08\times 10^{4} \right )=331488.696N/m^{2}$$

Total temperature,

$$T_{02}=T_{01}=\left ( \frac{T_{01}}{T_{1}} \right )T_{1}=4.2\times 229.74K=964.908K$$

Satellite orbit

$$\frac{{{r_{\max }}}}{{{r_{\min }}}} = \frac{{1 + e}}{{1 – e}} = \frac{{1 + 0.0014}}{{1 – 0.0014}} = 1.0028$$

$$\Rightarrow {r_{\max }} = {r_{\min }}\left( {1.0028} \right)$$

$${r_{\min }} = {\rm{radius}}\,{\rm{of}}\,{\rm{earth}}\,{\rm{ + }}\,{\rm{altitude}}\,{\rm{above}}\,{\rm{earth’s}}\,{\rm{surface}}$$

$$\Rightarrow {{\rm{r}}_{\min }} = 6.4 \times {10^6} + 0.4 \times {10^6} = 6.8 \times {10^6}\,m$$

$$\Rightarrow {r_{\max }} = 6.8 \times {10^6}\left( {1.0028} \right) = 681904\,m = 6.81904 \times {10^6}\,m$$

Therefore satellite’s altitude at apogee is

$$6.81904 \times {10^6} – 6.4 \times {10^6} = 419040\,m = 419.04\,km$$

Time period of the satellite is given as

$${T^2} = \frac{{4{\pi ^2}}}{{{k^2}}}{a^3}$$

$${k^2} = G{M_{earth}} = 3.986 \times {10^{14}}\,{m^3}/{s^2}$$

$$\Rightarrow a = {\rm{semi}}\,{\rm{major}}\,{\rm{axis}}\,{\rm{ = }}\frac{{{r_{\max }} + {r_{\min }}}}{2} = \frac{{6.81904 \times {{10}^6} + 6.8 \times {{10}^6}}}{2} = 6.80952 \times {10^6}\,m$$

$${T^2} = \frac{{4{\pi ^2}}}{{3.986 \times {{10}^{14}}}} \times {\left( {6.80952 \times {{10}^6}} \right)^3}$$

$$\Rightarrow T = 5592.242\,s = 1.5534\,hr$$

$${V_{perigee}} = {r_{\min }}\dot \theta$$

$$\dot \theta = \frac{h}{{{{\left( {{r_{\min }}} \right)}^2}}}$$

$${h^2} = {r_{\min }}\left( {1 + e} \right){k^2}$$

$$\Rightarrow {h^2} = \left( {6.8 \times {{10}^6}} \right)\left( {1 + 0.0014} \right)3.986 \times {10^{14}}$$

$$\Rightarrow h = 5.20987 \times {10^{10}}$$

Therefore,

$$\dot \theta = \frac{{5.20987 \times {{10}^{10}}}}{{{{\left( {6.8 \times {{10}^6}} \right)}^2}}} = 0.0011267\,rad/s$$

$${V_{perigee}} = \left( {6.8 \times {{10}^6} \times 0.0011267} \right) = 7661.56\,m/s = 7.66156\,km/s$$