When airplane is flying at \(Lift/Drag\) ratio of maximum , coefficient of drag at zero lift is equal to coefficient of induced drag.

\(Total\, drag = drag\, at\, zero\, lift + induced\, drag \)

\[{C_D} = {C_{D,0}} + {C_{D,i}}\]

Since \((L/D)\) is here maximum, therefore, \( coefficient\, of\, drag\, at\, zero\, lift =coefficient\, of\, induced\, drag\),

\[{C_{D,0}} = {C_{D,i}}\]

Therefore,

\[{C_D} = 2{C_{D,i}}\]

\[{C_{D,i}} = \frac{{C_L^2}}{{\pi eAR}}\]

\[L = \frac{1}{2}{\rho _\infty }V_\infty ^2S{C_L}\]

At, a steady level flight, \(L=W\)

\[ \Rightarrow {C_L} = \frac{{2W}}{{{\rho _\infty }V_\infty ^2S}} = \frac{{2 \times 23000}}{{1.225 \times {{\left( {90} \right)}^2} \times 20}} = 0.232\]

\[{C_{D,i}} = \frac{{C_L^2}}{{\pi eAR}} = \frac{{{{\left( {0.232} \right)}^2}}}{{\pi \times 0.9 \times 9}} = 0.0021\]

Therefore,

\[{C_D} = 2 \times \left( {0.0021} \right) = 0.0041\]

Total drag,

\[D = \frac{1}{2} \times {\rho _\infty } \times V_\infty ^2 \times S \times {C_{D}}\]

\[ \Rightarrow D = \frac{1}{2} \times 1.225 \times {\left( {90} \right)^2} \times 20 \times 0.0041 = 406.823\,N\]

Induced drag of the airplane, \({D_i} = {q_\infty }S{C_{{D_i}}}\)

Here,  \[{S} = 16\,{m^2}\]

\[{\rho _\infty } = 1.225\,kg/{m^3}\]

\[{V_\infty } = \left( {\frac{{260 \times 1000}}{{60 \times 60}}} \right) = 72.2\,m/s\]

\[{q_\infty } = \frac{1}{2}{\rho _\infty }V_\infty ^2\,\]

\[ \Rightarrow {q_\infty } = \frac{1}{2} \times \left( {1.225} \right) \times {\left( {72.2} \right)^2} = 3192.86\,N/{m^2}\]

\[L = W = 10000 = {q_\infty }S{C_L}\]

\[ \Rightarrow {C_L} = \frac{{10000}}{{{q_\infty }S}} = \frac{{10000}}{{\left( {3192.86} \right) \times 16}} = 0.1957\]

\[{C_{{D_i}}} = \frac{{C_L^2}}{{\pi eAR}} = \frac{{{{\left( {0.1957} \right)}^2}}}{{\pi \times 0.6 \times 7.4}} = 0.002746\]

Therefore,

\[{D_i} = {q_\infty }S{C_{{D_i}}} = 3192.86 \times 16 \times 0.002746 = 140.281\,N\]

Neutral point and static margin come in the context of longitudinal static stability.

Neutral point :

If the position center of gravity is allowed to move, with other things fixed like position of the aerodynamic center, then there will be a position of center of gravity where change in the coefficient of moment about this center of gravity with respect to the absolute angle of attack will be zero, that is\( \frac{{\partial {C_{M,cg}}}}{{\partial {\alpha _a}}} = 0\). There will be also positions of center of gravity when this will be negative or positive. When \(\frac{{\partial {C_{M,cg}}}}{{\partial {\alpha _a}}} = 0\), the position of center of gravity at this point is called neutral point. Neutral point is a fixed point on the aircraft. Center of gravity can move forward and aft of the neutral point. When the center of gravity is forward of the neutral point the aircraft has longitudinal static stability. If it is on the neutral point, it has neutral longitudinal stability, and if it is aft the neutral point it has longitudinal unstability.

Static margin :

It is the distance between the center of gravity and the neutral point of the aircraft, which is expressed with respect to the mean aerodynamic chord of the wing. For longitudinal static stability aircraft’s center of gravity must be forward of the neutral point, that is static margin should be positive. The larger the static margin, the more stable will be the airplane. Therefore, to make an aircraft more responsive to pilot inputs static margin is reduced, that is there will be a low static margin, for such airplanes.

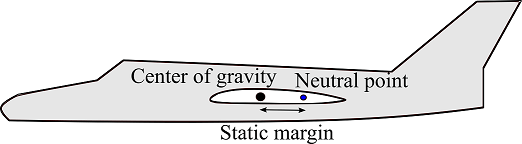Neutral point, center of gravity and static margin of an aircraft

Airfoil terminology 

Airfoil terminology

Mean camber line : It is an imaginary line which is halfway between the upper surface and the lower surface of the airfoil. It intersects the chord line at the leading and trailing edge of the airfoil, and it can curve above or below the chord line.

Leading edge :Leading edge is the point which is at the front of airfoil and it is the most forward point of the mean camber line. It has a maximum curvature or minimum radius at front of the airfoil.

Trailing edge: It is the point which is located at the trailing edge of the airfoil and is the most rearward point of the mean camber line. It is also the point of maximum curvature at the rear end of the airfoil.

Chord line : It is a straight line which connects the leading and trailing edge of the airfoil. Chord length or chord is the precise distance from the leading to the trailing edge of the airfoil.

Camber : It is a measure of curvature of the airfoil. it is the maximum distance which is measured perpendicular to the chord line between the mean camber line and the chord line.

Thickness : It varies along the chord of the airfoil.

NACA airfoil nomenclature :

NACA is National Advisory Committee for Aeronautics. It initially developed airfoil system which was numbered, giving a numerical designation to each airfoil. The shape of the airfoil can be described using the of digits which is followed by the word NACA.

NACA 4 digit series : Here, maximum camber, distance of the maximum camber and maximum thickness is defined in terms of the chord ‘c’. For example NACA 2412,

• First digit, 2, describes the maximum camber in hundredth of chord. For this airfoil maximum camber is 0.02c
• Second digit is the distance of the maximum camber from the leading edge of the airfoil in tenths of chord. For the above NACA  airfoil, distance of the maximum camber from the leading edge along the chord of the airfoil is 0.4c
• Last two digit gives maximum thickness of the airfoil in hundredths of chord. For the above NACA airfoil, maximum thickness of the airfoil is 0.12c

NACA 5 digit series : Here, the first digit gives the design lift coefficient, second digit gives the location of maximum camber, and last two digit gives the maximum thickness of the airfoil. For example, NACA 23012

• The first digit when multiplied by 3/2, gives the design lift coefficient in tenths. For this airfoil, design lift coefficient is (2 x 3/2=3, 3/10=0.3).
• The next two digit when divided by 2 gives the location of maximum camber from the leading edge of the airfoil in hundredths of chord. For this airfoil, location of maximum camber from the leading edge of the airfoil along chord is (30/2 = 15,= 15c/100=0.15c)
• The last two digit gives the maximum thickness in hundredths of chord . For the above airfoil, maximum thickness of the airfoil is 0.12c

NACA 6 digit series : These are also called laminar flow airfoils. Here, more importance was given to maximise the laminar flow on the airfoil. First digit indicates the series, second digit gives the the location of minimum pressure, third digit gives the design lift coefficient, last two digit gives the maximum thickness . Consider a 6 digit NACA   airfoil, NACA 64212

• 6 – It is the NACA series designation.
• Second digit gives the location of minimum pressure in tenths of chord for a basic symmetric thickness distribution at zero lift. For this airfoil, location of minimum pressure is at 0.4c from the leading edge.
• Third digit gives the design lift coefficient in tenths. For this airfoil, design lift coefficient is 0.2
• Last two digit gives the the maximum thickness in hundredths of chord. For the above airfoil maximum thickness of the airfoil is 0.12c 

NACA 7 digit series : 7 digit series NACA airfoils had more laminar flow. Here, 7 is the series designation. It indicates location of minimum pressure on upper and lower surface of the airfoil, thickness distribution and mean camber line forms, design lift coefficient, and airfoil maximum thickness. For example NACA 747A315

• Here first digit gives series designation.
• Second digit gives the location of minimum pressure on the upper surface of airfoil in tenths of chord. For this airfoil this is 0.4c
• Third digit gives the location of minimum pressure on lower surface of the airfoil in tenths of chord. For this airfoil it is 0.7c
• The forth one which is a letter gives thickness distribution and mean line forms used. For this airfoil it is ‘A’.
• Fifth digit gives the design lift coefficient in tenths. For this airfoil it is 0.3
• Last digit gives the maximum thickness in hundredths of chord. For this airfoil it is 0.15c

NACA 8 digit series : These were called supercritical airfoils, maximising the laminar flow on upper and lower surface of the airfoil. The naming convention is similar to the 7 digit series, except that that the series begins with 8. For example NACA 835A216 

• Here, 8 designates the series
• Location of minimum pressure on upper surface of airfoil is at 0.3c
• Location of minimum pressure on lower surface of the airfoil is 0.5c
• ‘A’ gives the thickness distribution and mean line forms.
• Design lift coefficient for this airfoil is 0.2
• maximum thickness of the airfoil is 0.16c

NACA 1 digit or 16 digit series : 1 digit series is identified with 5 digits. Here, the digits indicates location of minimum pressure, design lift coefficient and maximum thickness. For example NACA 16-123

• Here, the first digit ‘1’ is the series designation.
• Second digit gives the location of minimum pressure in tenths of chord from the leading edge. For this airfoil it is 0.6c
• Third digit gives the design lift coefficient in tenths. For this airfoil it is 0.1
• Last two digit gives the maximum thickness of the airfoil in hundredths of chord. For this airfoil it is 0.23c 

Rate of climb : Let an airplane is flying at an angle of ‘\(\theta\)’ to the horizontal. Lift on the aircraft is perpendicular to the flight velocity and drag is parallel. Weight of the aircraft will be acting perpendicular to the horizontal. Thrust of the aircraft will be aligned to the flight path. So here, thrust on the aircraft will be acting to overcome drag and a component of weight which is \(W\sin \theta \) .

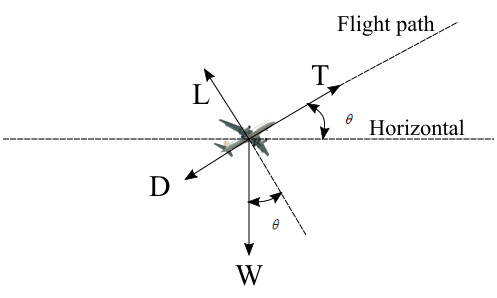Airplane climbing in atmosphere

\(T = D + W\sin \theta \)

Also, here lift will be, \(L = W\cos \theta \)

On multiplying both side of thrust equation with \({V_\infty }\),

\[T{V_\infty } = D{V_\infty } + W{V_\infty }{\sin \theta } \]

\[\Rightarrow \frac{{T{V_\infty } – D{V_\infty }}}{W} = {V_\infty }\sin \theta\]

\(V_\infty\sin \theta \) is  the rate of climb since it is the vertical velocity of the airplane. Supersonic aircrafts have high accelerated rates of climb. We can calculate the rate of climb of such aircraft by using the energy method.

\[\frac{{d{H_s}}}{{dt}} = \frac{{dh}}{{dt}} + \frac{V}{g}\frac{{dV}}{{dt}}\]

Where \({H_s}\) is the specific energy of the aircraft.

Turn rate : Suppose an aircraft makes a level turn with a bank angle \(\prime \psi \prime \). In the level turn weight of the aircraft will be equal to \(L\cos \psi \), that is, \[W = L\cos \psi\] There will be a force which will act towards the radius of the circular turn produced by the resultant of lift and weight. This force is \(F = \sqrt {{L^2} – {W^2}}\), also, from Newton’s second law of motion, \[F = m\frac{{V_\infty ^2}}{R}\]

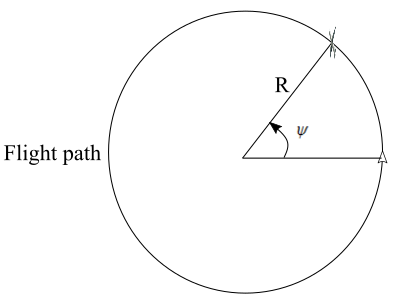A level turn of an airplane in flight on a horizontal plane

therefore,

\[ m\frac{{V_\infty ^2}}{R} = \sqrt {{L^2} – {W^2}} \]

\[ \Rightarrow \frac{W}{g}\frac{{V_\infty ^2}}{R} = \sqrt {{L^2} – {W^2}}\]

\[ \Rightarrow R = \frac{{WV_\infty ^2}}{{g\sqrt {{L^2} – {W^2}} }}\]

turn rate is \(\frac{{{V_\infty }}}{R} = \omega \), therefore,

\[\omega = \frac{{g\sqrt {{L^2} – {W^2}} }}{{W{V_\infty }}}\]

This turn rate is for a level turn on a horizontal plane. For other types of aircraft maneuver force created by the resultant of lift and weight will be different and therefore turn rate will be different.

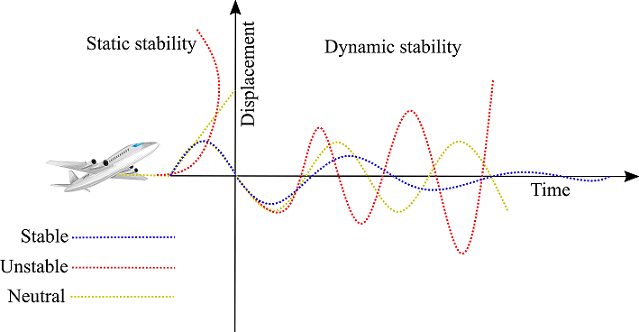
Static stability : If an aircraft in flight is disturbed from its equilibrium state, for example by a gust and the aircraft has its initial tendency to return to its equilibrium state, then the aircraft is having a static stability. Static stability can be divided into statically stable system, statically unstable system and statically neutral system.

Statically stable system (positive static stability) : Aircraft has initial tendency to return to its equilibrium position.

Statically unstable system (Negative static stability) : Aircraft has its initial tendency to move away from its equilibrium position.

Statically neutral system (Neutral static stability) : Aircraft has a tendency to maintains its original disturbed position.

Dynamic stability : When an aircraft is disturbed from its equilibrium position in flight it first go through static stability and later the time history of the aircraft’s motion and attitude makes up the dynamic stability. So dynamic stability is the decay of the amplitude of response over a finite time which has been occurred due to disturbance to reach the equilibrium state.

Dynamic stability can be divided into dynamically stable system, dynamically unstable system, and dynamically neutral system.

Dynamically stable system (Positive dynamic stability ): Aircraft has tendency to return to its equilibrium position through damping of oscillations.

Dynamically unstable system (Negative dynamic stability ) : Aircraft oscillates with increased amplitudes and equilibrium position is never reached.

Dynamically neutral system (Neutral dynamic stability ) :  Aircraft maintains uniform oscillations with a constant amplitude.

Static and dynamic stability of aircraft

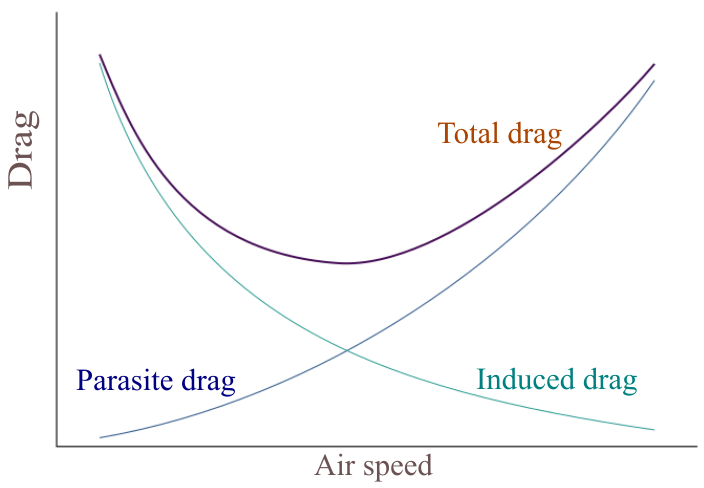
Parasite drag :  Induced drag is the drag which results from the lift force which is produced by an aircraft in flight. Parasite drag is the combination of pressure drag and skin friction drag. It is called parasite drag because it is not produced on generation of lift and so parasite in nature. Pressure drag also known as Form drag is caused due to the boundary layer separation which in turn depends on the shape of the object. Skin friction drag is caused due to the skin friction between the object and the moving fluid, that is air, which comes in  contact.

Profile drag : Profile drag is the same term for parasite drag when it is used for an aircraft’s wing.

Induced drag : Induced drag which is also called drag due to lift, is produced due to the redirection of airflow which results in generation of vortex. It occurs on lift generating surfaces like aircraft’s wing. The generation of vortex results in downwash.  Amount of induced downwash affects the induced drag.

Drag components

Wave drag : Wave drag is the drag which is produced when there is a formation of shock waves. Shock waves are produced when  aircraft is flying at a transonic or supersonic speed. Wave drag is a sudden increase in drag when the aircraft speed crosses critical mach number. Sound barrier is a result of wave drag.

Ground effect is the floating of an aircraft when it is near the ground on landing. “Ground effect” generally comes into “effect” when the aircraft’s height from the ground is nearly half-the length of the aircraft’s wingspan.

When an aircraft flies it creates wing tip vortices. On approaching to the ground during landing, the strength of wing tip vortices get diminished, because of interaction with the ground. Wing tip vortices creates downwash which results in induced drag. Since, strength of the wing tip vortices is reduced, therefore, the downwash and strength of the induced drag is reduced. This is called the ground effect which results in airplane’s tendency to “flare” and float above ground when the aircraft is at the moment of landing.

The reduced drag can be accounted by an expression, given by McCormick as \[\alpha = \frac{{{{\left( {16a/b} \right)}^2}}}{{1 + {{\left( {16a/b} \right)}^2}}}\]

Here,  ‘a‘ is the height of the airplane’s wing above the ground and ‘b‘ is the span of the wing. Here, Induced drag will be reduced by a factor ‘\(\alpha \)’ which is less than or equal to one.

Induced drag is \[{C_{D,i}} = \alpha \frac{{C_L^2}}{{\pi eAR}}\]

Application of ground effect

Reynolds number is the ratio of inertial force to viscous force. A boundary layer is a layer where the behavior of these forces get change.\[Re = \frac{{\rho VL}}{\mu } = \frac{{VL}}{\nu }\] Here, \(\rho \) is the density, \(V\) is the flow speed, \(L\) is the characteristic linear dimension, \(\mu\) is the dynamic viscosity of the fluid, and \(\nu\) is the kinematic viscosity of the fluid.

Laminar flows are smooth flow. It occurs at low Reynolds numbers. Here viscous forces are dominant. Turbulent flows have chaotic eddies, there are vortices, and inflow instabilities. They have a higher Reynolds number. There is a transition from a laminar flow to turbulent flow in a flow field and the Reynolds number at which it occurs is known as a critical Reynolds number. Reynolds number is also used to manage the scaling effect. For example, an airfoil in a wind tunnel test is small as compared to its original size in wings of the aircraft. Matching their Reynolds number is required to get a similar characteristics.

Flows over geometrical similar bodies having same Reynolds and Mach number are dynamic similar, and lift, drag and moment coefficients for these bodies will be identical.

A canard is a small wing that is placed forward of the main wing of a fixed-wing aircraft. A canard is used for longitudinal stability and control. Canard can be of fixed type, movable, or of variable geometry surface. A canard is used for the production of lift, pitch control, longitudinal stability, or trim. It modifies the airflow over the main wing. Canard influences aircraft’s longitudinal equilibrium, and static and dynamic stability characteristics.

Canard in front of the main wing