624
Points
Questions
72
Answers
119
-
Asked on 9th November 2020 in Aeronautics.
Ground effect is the floating of an aircraft when it is near the ground on landing. “Ground effect” generally comes into “effect” when the aircraft’s height from the ground is nearly half-the length of the aircraft’s wingspan.
When an aircraft flies it creates wing tip vortices. On approaching to the ground during landing, the strength of wing tip vortices get diminished, because of interaction with the ground. Wing tip vortices creates downwash which results in induced drag. Since, strength of the wing tip vortices is reduced, therefore, the downwash and strength of the induced drag is reduced. This is called the ground effect which results in airplane’s tendency to “flare” and float above ground when the aircraft is at the moment of landing.
The reduced drag can be accounted by an expression, given by McCormick as \alpha = \frac{{{{\left( {16a/b} \right)}^2}}}{{1 + {{\left( {16a/b} \right)}^2}}}
Here, ‘a‘ is the height of the airplane’s wing above the ground and ‘b‘ is the span of the wing. Here, Induced drag will be reduced by a factor ‘\alpha ’ which is less than or equal to one.
Induced drag is {C_{D,i}} = \alpha \frac{{C_L^2}}{{\pi eAR}}
- 1302 views
- 1 answers
- 0 votes
-
Asked on 17th August 2020 in Fluid dynamics.
Reynolds number is the ratio of inertial force to viscous force. A boundary layer is a layer where the behavior of these forces get change.Re = \frac{{\rho VL}}{\mu } = \frac{{VL}}{\nu } Here, \rho is the density, V is the flow speed, L is the characteristic linear dimension, \mu is the dynamic viscosity of the fluid, and \nu is the kinematic viscosity of the fluid.
Laminar flows are smooth flow. It occurs at low Reynolds numbers. Here viscous forces are dominant. Turbulent flows have chaotic eddies, there are vortices, and inflow instabilities. They have a higher Reynolds number. There is a transition from a laminar flow to turbulent flow in a flow field and the Reynolds number at which it occurs is known as a critical Reynolds number. Reynolds number is also used to manage the scaling effect. For example, an airfoil in a wind tunnel test is small as compared to its original size in wings of the aircraft. Matching their Reynolds number is required to get a similar characteristics.
Flows over geometrical similar bodies having same Reynolds and Mach number are dynamic similar, and lift, drag and moment coefficients for these bodies will be identical.
- 1381 views
- 1 answers
- 0 votes
-
Asked on 15th July 2020 in Flight mechanics.
A canard is a small wing that is placed forward of the main wing of a fixed-wing aircraft. A canard is used for longitudinal stability and control. Canard can be of fixed type, movable, or of variable geometry surface. A canard is used for the production of lift, pitch control, longitudinal stability, or trim. It modifies the airflow over the main wing. Canard influences aircraft’s longitudinal equilibrium, and static and dynamic stability characteristics.
 Canard in front of the main wing
Canard in front of the main wing- 1384 views
- 1 answers
- 0 votes
-
Asked on 15th July 2020 in Aeronautics.
Runway
According to the ICAO-International Civil Aviation Organisation-Runway is defined as a “defined rectangular area on a land aerodrome prepared for the landing and takeoff of aircraft.” Runways can be man-made or natural. Man-made runways are made of asphalt, concrete, or a mixture of both. Natural runways can be of grass, sand, ice, dirt, salt, or gravel.
Runways are named based on the magnetic azimuth of the runways heading which are in decadegrees. Runways are named using numbers between 01 and 36. A runway which is numbered 09 points east (90 degrees), runway 18 is south (180 degrees), runway 27 ( 270 degrees) points west, and runway 36 points north (360 degrees). A runway which is used in both directions is named for each direction separately.Runway lengths can be of short to long such as between 245 m to 5500 m.
Taxiway
It is a path for an aircraft which connects the runway with terminals, hangers and aprons, and other facilities. It is made up of concrete or asphalt. It is also made up of gravels and grass in smaller airports.
A permanent classification number with a combination of aircraft classification number is used to indicate the strength of runway, taxiway, or an airport apron.
- 1577 views
- 1 answers
- 0 votes
-
Asked on 2nd July 2020 in Flight mechanics.
Objects and astronauts appear to float around on International Space Station. Gravity also exists in space, that is the reason why the moon moves around earth or earth is orbiting around the Sun. If a tower is made to height of ISS and any object is thrown, it will definitely hit the ground. Space station and objects in it or satellites are also falling towards the earth. However, since they have huge orbital velocity, they don’t fall on the earth. They are falling around the earth. The circular orbital velocity around earth is 7.9 km/s. Satellites and International Space Station are designed to move around the earth and stay in orbit. Since they are in orbit they are in free fall and is weightless.
- 1130 views
- 1 answers
- 0 votes
-
Asked on 29th June 2020 in Aeronautics.
Rudder is the primary control surface of an aircraft. Rudder is attached at the rear end of the fuselage of the aircraft. The main function of the vertical stabilizer is to provide stability to the aircraft. The vertical stabilizer prevents side to side or yawing motion of the aircraft nose. The rudder which is attached to the vertical stabilizer by hinges produces a varying amount of force that is used to generate and control the yawing motion.
Rudder also helps during the motion of the aircraft. Aircraft gets turn by banking the aircraft with the use of ailerons or spoilers. Here rudder ensures that aircraft are properly aligned to the flight path.
The torque generated depends on the lift produced by the amount of deflection of the rudder. The side force or lift is generated through the center of pressure of the vertical stabilizer which is at some distance from the aircraft’s center of gravity.
- 1684 views
- 1 answers
- 0 votes
-
Asked on 17th June 2020 in Aerodynamics.
In an airfoil, there is a two-dimensional flow. In a wing, there is three-dimensional flow. In an aircraft wing lift is generated by a pressure difference, where there is a high pressure on the bottom surface and a low pressure on the top surface of the wing. This net imbalance creates lift, however, due to this pressure imbalance there is flow near the wingtip, which tends to curl, the flow of air tends to curl around tips, being forced from high-pressure region just underneath the tips to the top of the low-pressure region.
The flow gets circulatory motion and trails downstream of the wing, which is called a trailing vortex. These vortices induce a downward component of velocity, called downwash near the wing. Downwash inclines the local relative wind in the downward direction. A local lift vector is created perpendicular to the local relative wind, and there is a component of the local lift vector in the direction of the local relative wind which is a drag. This drag is called induced drag. In aerodynamics, the induced drag is also called lift-induced drag, vortex drag, or drag due to lift.
- 1255 views
- 1 answers
- 0 votes
-
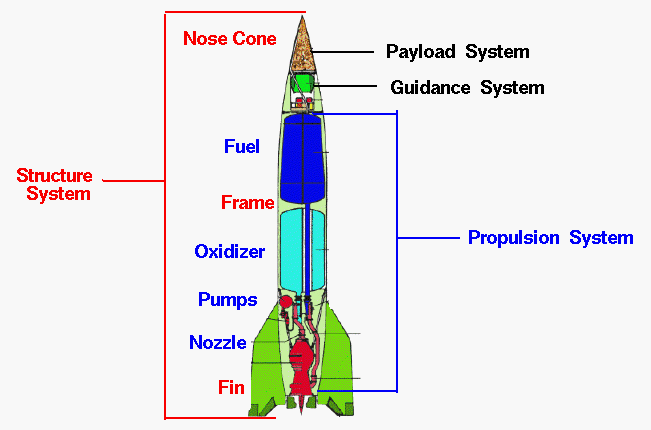
Asked on 5th June 2020 in Rocket and Space propulsion.
A rocket is a device which produces thrust with the help of a propulsion system to carry a payload. The propulsion system consists of fuel and oxidizer. Both fuel and oxidizer are contained inside the rocket. Unlike in the aircraft where the surrounding air is used for combustion purposes in the combustion chamber, rockets carry both oxidizer and fuel with it. Aircraft engines are called air-breathing engines. Rocket engines are called non-air-breathing engines. In the rocket, the combustion process happens through the combustion of fuel and oxidizer which are called propellants. Rocket works on the principle of Newton’s third law of motion, which states that for every action there is an equal and opposite reaction. Combustion exhaust of high temperature and pressure passes with a very high velocity from the rocket nozzle, which produces an upward thrust. Rockets are of a single stage or multiple stages. Rockets are used to carry payloads like satellites, however, if the payload is a warhead it is called a missile.
- 1338 views
- 1 answers
- 0 votes
-
Asked on 15th May 2020 in Aerospace.
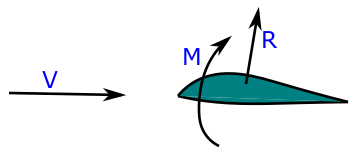
Aerodynamic forces and moments on a body arises from two basic sources; pressure distribution and shear stress distribution over the body surface. Pressure force comes from the air whereas shear force comes due to the friction between the body and the air.
Both pressure and shear stress distribution over the complete body creates a resultant aerodynamic force R.
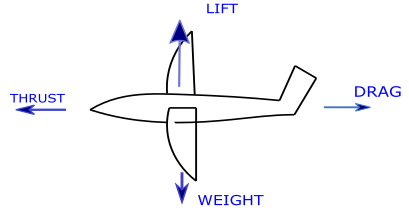
Lift is the component of R which is perpendicular to free stream velocity. Whereas drag is a component of R which is parallel to free stream velocity.
Lift force counteracts the weight when an aircraft is in air. Lift force is mostly generated by the wings, while there is also small contribution of rest parts of the aircraft like horizontal stabiliser and fuselage.
Drag force is a force which opposes the thrust force produced by the aircraft engines.
- 1557 views
- 1 answers
- 0 votes
-
Asked on 12th November 2019 in Flight mechanics.
Lift slope for the wing is a=\frac{a_{0}}{1+\frac{a_{0}}{\pi AR}\left ( 1+\tau \right )}.Here a_{0}=0.1080/\textrm{degree}=6.188\;\textrm{per radian}.\delta =\tau=0.054.Therefore a=\frac{6.188}{1+\frac{6.188}{\pi(8)}\left ( 1+0.054 \right )}=4.91/\textrm{rad}=0.0857\;\textrm{per degree}
Coefficient of lift is given as C_{L}=a\left ( \alpha-\alpha_{L=0} \right ) \\=0.0857\left ( 7-\left ( -1.3 \right ) \right ) \\=0.712
Induced drag coefficient is given as C_{D,i}=\frac{C_{L}^{2}}{\pi AR}\left ( 1+\delta \right )=\frac{0.712^{2}}{\pi(8)}\left ( 1.054 \right ) \\=0.0212
- 3705 views
- 1 answers
- 0 votes