Rate of climb : Let an airplane is flying at an angle of ‘\(\theta\)’ to the horizontal. Lift on the aircraft is perpendicular to the flight velocity and drag is parallel. Weight of the aircraft will be acting perpendicular to the horizontal. Thrust of the aircraft will be aligned to the flight path. So here, thrust on the aircraft will be acting to overcome drag and a component of weight which is \(W\sin \theta \) .

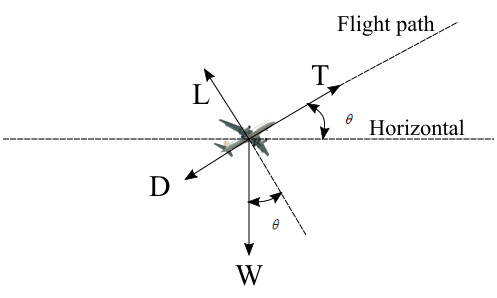Airplane climbing in atmosphere

\(T = D + W\sin \theta \)

Also, here lift will be, \(L = W\cos \theta \)

On multiplying both side of thrust equation with \({V_\infty }\),

\[T{V_\infty } = D{V_\infty } + W{V_\infty }{\sin \theta } \]

\[\Rightarrow \frac{{T{V_\infty } – D{V_\infty }}}{W} = {V_\infty }\sin \theta\]

\(V_\infty\sin \theta \) is  the rate of climb since it is the vertical velocity of the airplane. Supersonic aircrafts have high accelerated rates of climb. We can calculate the rate of climb of such aircraft by using the energy method.

\[\frac{{d{H_s}}}{{dt}} = \frac{{dh}}{{dt}} + \frac{V}{g}\frac{{dV}}{{dt}}\]

Where \({H_s}\) is the specific energy of the aircraft.

Turn rate : Suppose an aircraft makes a level turn with a bank angle \(\prime \psi \prime \). In the level turn weight of the aircraft will be equal to \(L\cos \psi \), that is, \[W = L\cos \psi\] There will be a force which will act towards the radius of the circular turn produced by the resultant of lift and weight. This force is \(F = \sqrt {{L^2} – {W^2}}\), also, from Newton’s second law of motion, \[F = m\frac{{V_\infty ^2}}{R}\]

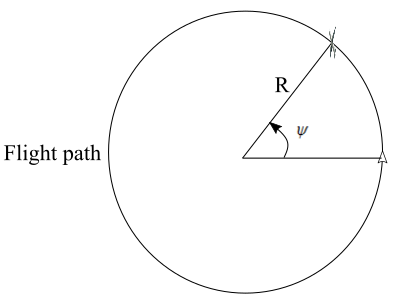A level turn of an airplane in flight on a horizontal plane

therefore,

\[ m\frac{{V_\infty ^2}}{R} = \sqrt {{L^2} – {W^2}} \]

\[ \Rightarrow \frac{W}{g}\frac{{V_\infty ^2}}{R} = \sqrt {{L^2} – {W^2}}\]

\[ \Rightarrow R = \frac{{WV_\infty ^2}}{{g\sqrt {{L^2} – {W^2}} }}\]

turn rate is \(\frac{{{V_\infty }}}{R} = \omega \), therefore,

\[\omega = \frac{{g\sqrt {{L^2} – {W^2}} }}{{W{V_\infty }}}\]

This turn rate is for a level turn on a horizontal plane. For other types of aircraft maneuver force created by the resultant of lift and weight will be different and therefore turn rate will be different.