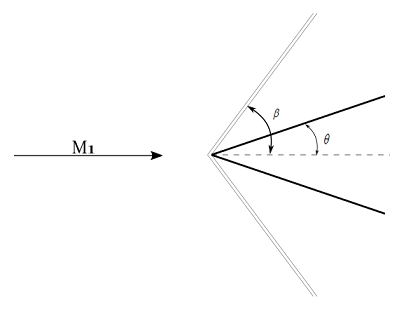
A flow is passing over a {20^ \circ } half-angle wedge having a upstream Mach number, pressure and temperature of 2.8,\,1\,atm\, and 310\,K. Find the wave angle and downstream Mach number, pressure and temperature.
A flow is passing over a {20^ \circ } half-angle wedge having a upstream Mach number, pressure and temperature of 2.8,\,1\,atm\, and 310\,K. Find the wave angle and downstream Mach number, pressure and temperature.
Wave angle can be found from \theta -\beta -M diagram. For deflection angle \theta =20^{\circ} and Mach number, M_{1}=2.8 , wave angle \beta =39.5^{\circ}.
Therefore, normal component of upstream Mach number,
M_{n1}=M_{1}Sin\beta = 2.8Sin\left ( 39.5^{\circ} \right )=1.78
From normal shock properties table, for M_{n1}=1.78,
\frac{p_{2}}{p_{1}}=3.530,\frac{T_{2}}{T_{1}}=1.517,M_{n2}=0.6210
Therefore, Downstream pressure, p_{2}=\left ( \frac{p_{2}}{p_{1}} \right )p_{1}=\left ( 3.530 \right )\left ( 1\,atm \right )=3.53\,atm
Downstream temperature, T_{2}=\left ( \frac{T_{2}}{T_{1}} \right )T_{1}=\left ( 1.517 \right )310=470.27\,K
Downstream Mach number, M_{2}=\frac{M_{n2}}{sin\left ( \beta -\theta \right )}=\frac{0.6210}{Sin\left ( 39.5-20 \right )}=1.86