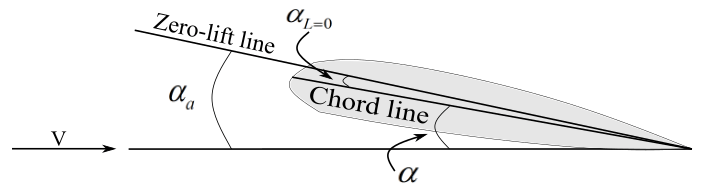
Angle of attack: For an airfoil, it is the angle between the chord line and the direction of the relative wind. In general, angle of attack is the angle between a reference line on the airplane or wing and the relative wind. The reference line can be a chord line in case of an airfoil, a line from leading edge to trailing edge at some average point on wing, or a centerline of a fuselage.

Reference line does not make any difference if it is used consistently. An increase in angle of attack increases the coefficient of lift up to a point. This point is called the critical angle of attack. If the angle of attack is increased beyond this critical angle, stall takes place and there is a decrease in coefficient of lift.

Absolute angle of attack: It is the angle between the zero-lift line and the relative wind. Zero-lift line is a line through an airfoil when zero lift is produced. The zero-lift line is drawn from the trailing edge and is parallel to the relative wind. The airfoil is at zero-lift angle of attack. Zero-lift line is symmetric with chord for a symmetrical airfoil. For a cambered airfoil, the zero-lift line lies above the chord line, as the zero-lift angle of attack is negative for such airfoils. Absolute angle of attack is the sum of the angle of attack and angle of attack at zero-lift. If the absolute angle of attack is zero, then the lift is zero, for any cambered airfoil.

Absolute angle of attack

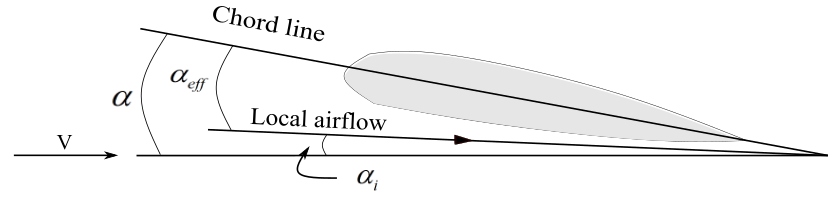
Induced angle of attack: Induced angle of attack is associated with the induced drag. Induced drag is due to trailing edge vortex, which creates downwash. Downwash deflects the free-stream air downward, in the vicinity of the wing. This deflection is the ‘induced angle’ and it is the difference between the local airflow direction of the wing and free-stream airflow direction. So, at the vicinity of the wing, an airfoil sees an effective angle of attack which is less than the angle of attack seen through the naked eye, \(\alpha _{eff} = \alpha \ -\ {\alpha _i}\).

Induced angle of attack