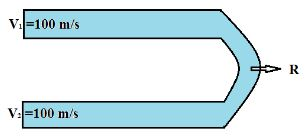
Consider a length of pipe bent into a U-shape. The inside diameter of the pipe is 0.5\;m. Air enters one leg of the pipe at a mean velocity of 100\; m/s and exits the other leg at the same magnitude of velocity, but moving in the opposite direction. Calculate the magnitude and direction of the force exerted on the pipe by the airflow.
Consider a length of pipe bent into a U-shape. The inside diameter of the pipe is 0.5\;m. Air enters one leg of the pipe at a mean velocity of 100\; m/s and exits the other leg at the same magnitude of velocity, but moving in the opposite direction. The pressure of the flow at the inlet and exit is the ambient pressure of the surroundings. Calculate the magnitude and direction of the force exerted on the pipe by the airflow. The air density
is 1.23\; kg/m^{3}.
Length of the pipe is bent into ‘U’ shape.Here inside diameter = 0.5 \;m and air density = 1.23\;kg/m^{3}.
‘-R’ exerted by the pipe, reverses the flow velocity.Cross sectional area = \frac{\pi\;d^{2}}{4}
A=\frac{\pi d^{2}}{4} \\=\frac{\pi (0.5)^{2}}{4} \\=0.196\;m^{2}
Mass flow entering the pipe is \dot{m}=\rho _{1}A_{1}V_{1}=1.23\times 0.196\times 100 \\=24.11\;kg/sec \\R=-\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc} \left ( \rho V\cdot ds \right )V \\V_{2}=-V_{1} \\R=-\left [ -\dot{m} V_{1}+\dot{m}V_{2}\right ]=\dot{m}\left ( V_{1}-V_{2} \right ) \\=\dot{m}\left [ V_{1}-\left ( -V_{1} \right ) \right ]=\dot{m}2V_{1} \\R=24.11\times 2\times 100 \\=4822\;N