A velocity field is given by \(u=x^{2} + y\) and \(v= x^{3} + 2y\). Find the circulation around a closed contour which is defined by \(x = 1, y = 0, y = 1\) and \( x = 0\). Units of \(u\) and \(v\) are in \(m/s\).
A velocity field is given by \(u=x^{2} + y\) and \(v= x^{3} + 2y\). Find the circulation around a closed contour which is defined by \(x = 1, y = 0, y = 1\) and \( x = 0\). Units of \(u\) and \(v\) are in \(m/s\).
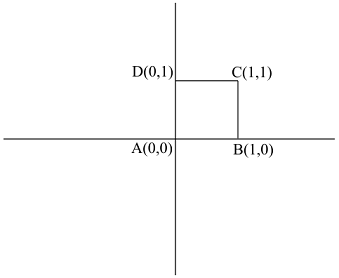Circulation around a rectangular contour
The closed contour is a square and its corner are at \(A(0,0), B(1,0), C(1,1), D(0,1)\).
Circulation is given by \[ \Gamma =\int _{ABCD}udx + vdy\]
\[\Rightarrow\Gamma = \int_{A}^{B}udx + \int_{B}^{C}vdy+\int_{C}^{D}udx+\int_{D}^{A}vdy\]
\[=\int_{0}^{1}\left ( x^{2}+y \right )dx +
\int_{0}^{1}\left ( x^{3}+2y \right )dy+\int_{1}^{0}\left ( x^{2}+ y \right )dx + \int_{1}^{0}\left ( x^{3}+2y \right )dy\] In the first integral, \(y=0\), in second integral \(x=1\), in the third integral, \(y=1\) and in the fourth integral \(x=0\).
\[=\int_{0}^{1}\left ( x^{2} \right )dx +
\int_{0}^{1}\left ( 1 + 2y \right )dy + \int_{1}^{0}\left ( x^{2} + 1 \right )dx + \int_{1}^{0}\left ( 2y \right ) dy\]
\[=\left | \frac{x^{3}}{3} \right |_{0}^{1}+\left | y+
\frac{2y^{2}}{2} \right |_{0}^{1}+\left | \frac{x^{3}}{3} + x \right |_{1}^{0}+\left | \frac{2y^{2}}{2} \right |_{1}^{0}\]
\[=\left [ \frac{1}{3} \right ]+\left [ 1+1 \right ]+\left [ -\frac{1}{3}-1 \right ]+\left [ -1 \right ]=0\]
