Find the circulation around a spinning circular cylinder in free stream flow of velocity \(40\,m/s\) at a standard sea level conditions, if the lift produced by the cylinder is \(8\,N/m\) of span.
Find the circulation around a spinning circular cylinder in free stream flow of velocity \(40\,m/s\) at a standard sea level conditions, if the lift produced by the cylinder is \(8\,N/m\) of span.
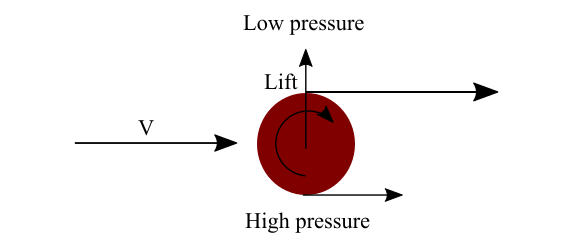
Lift per unit span produced by a circular cylinder with circulation, \(\tau\), is \[L^\prime=\rho _{\infty} v_{\infty }\tau\] This is also called the Kutta-Joukowski theorem. A spinning cylinder has a higher velocity at the top surface and a lower velocity at the bottom surface. Therefore, pressure at the top surface of the cylinder is lower than the bottom. This pressure difference creates a net upward force, which is called lift.
Since,\[L^{\prime}=\rho _{\infty} v_{\infty }\tau\]\[\Rightarrow 8=1.225\times 40\times \tau\]\[\Rightarrow \tau = 0.1633\]Therefore, circulation around the spinning circular cylinder is \(0.1633\, m^{2}/s\) .