Lift-curve slope for an airfoil

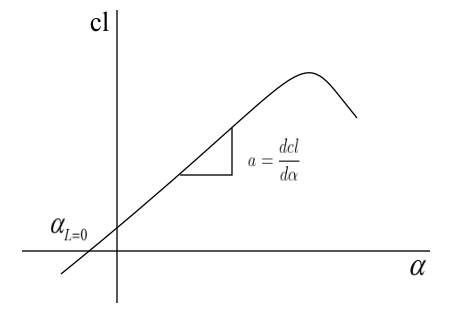
From the figure, Lift slope with respect to zero lift angle of attack, $a = \frac{dcl}{d\alpha }$ $$\Rightarrow a = \frac{c_{l} – c_{l,0}}{\alpha – \alpha _{L=0}}$$ $$\Rightarrow a = \frac{c_{l} – 0}{\alpha – \alpha _{L=0}}$$ $$\Rightarrow a = \frac{c_{l}}{\alpha – \alpha _{L=0}}$$ $$c_{l} = a\left ( \alpha – \alpha _{L=0} \right )$$ Therefore, at an angle of attack of $5^{\circ}$, when the airfoil is right-side-up, coefficient of lift is $$c_{l} = 0.1\left \{ 5^{\circ} – \left ( -3.5^{\circ} \right ) \right \}$$ $$=0.1\left \{ 8.5^{\circ} \right \}$$ $$=0.85$$ When, the airfoil is turned upside-down, its zero-lift angle of attack is $3.5^{\circ}$. Therefore, coefficient of lift in this condition at $5^{\circ}$ angle of attack is, $$c_{l} = 0.1\left ( 5^{\circ} – 3.5^{\circ} \right )$$ $$= 0.1\left ( 1.5^{\circ} \right )$$ $$= 0.15$$

Up-side and Inverted airfoil

At this condition, to generate the same amount of lift as when the airfoil was right-side-up at $5^{\circ}$ angle of attack, can be found as $$c_{l} = a\left ( \alpha – \alpha _{L = 0} \right )$$ $$\Rightarrow 0.85 = 0.1\left ( \alpha – 3.5^{\circ} \right )$$ $$\Rightarrow \alpha = 12^{\circ}$$ Therefore, an airfoil can fly upside-down. An airplane can also make an inverted flight, provided its angle of attack is more, in order to generate the same amount lift. In order to increase the angle of attack, an airplane’s nose can be pointed more skyward during the inverted flight.

An aircraft in an inverted flight