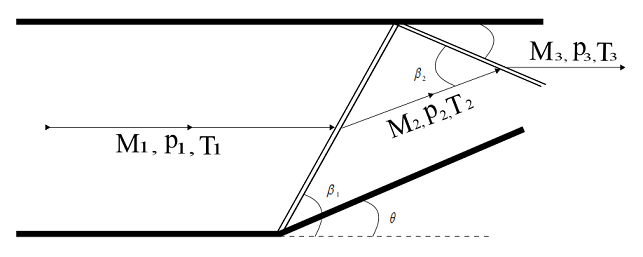
An oblique shock wave is generated at a compression corner having a deflection angle of 20^{^{\circ}}. The oblique shock wave is reflected from a straight horizontal wall which is present above the compression corner. The upstream flow properties are M_{1}=3.4,\,p_{1}=1\,atm,\,T_{1}=300\,K. Find the Mach number, pressure and temperature behind the reflected shock wave and angle made by the reflected shock wave with the upper wall.
An oblique shock wave is generated at a compression corner having a deflection angle of 20^{^{\circ}}. The oblique shock wave is reflected from a straight horizontal wall which is present above the compression corner. The upstream flow properties are M_{1}=3.4,\,p_{1}=1\,atm,\,T_{1}=300\,K. Find the Mach number, pressure and temperature behind the reflected shock wave and angle made by the reflected shock wave with the upper wall.
Wave angle \beta _{1} can be obtained from the \theta\, -\beta\, – M diagram. For, deflection angle of 20^{^{\circ}} and Mach number M_{1} of 3.4, \beta _{1}=35^{^{\circ}}
Therefore,
M_{n1}=M_{1}Sin\beta _{1} = 3.4Sin35^{^{\circ}}=1.95
For a normal shock wave for M_{n1}=1.95,
\frac{p_{2}}{p_{1}}=4.27, \frac{T_{2}}{T_{1}}=1.6473 and M_{n2}=0.586
Therefore,
M_{2}=\frac{M_{n2}}{Sin\left ( \beta _{1}-\theta \right )}=\frac{0.586}{Sin\left ( 35^{^{\circ}}-20^{^{\circ}} \right )}=2.26
For the reflected shock, from \theta -\beta\, – M diagram, for M_{2}=2.26 and \theta = 20^{^{\circ}} , wave angle, \beta _{2}=46.75^{^{\circ}}
Therefore,
M_{n2}=M_{2}Sin\beta _{2} = 2.26Sin46.75^{^{\circ}}=1.65
For a normal shock wave, for M_{n2}=1.56
\frac{p_{3}}{p_{2}}=3.001, \frac{T_{3}}{T_{2}}=1.423 and M_{n3}=0.654
Therefore,
M_{3}=\frac{M_{n3}}{Sin\left ( \beta _{2}-\theta \right )}=\frac{0.654}{Sin\left ( 46.75^{\circ}-20^{\circ} \right )}=1.453
and p_{3}=\left ( \frac{p_{3}}{p_{2}} \right )\left ( \frac{p_{2}}{p_{1}} \right )\left ( p_{1} \right )=\left ( 3.001 \right )\left ( 4.27 \right )\left ( 1 \right )=12.814\,atm
and T_{3}=\left ( \frac{T_{3}}{T_{2}} \right )\left ( \frac{T_{2}}{T_{1}} \right )\left ( T_{1} \right )=\left ( 1.423 \right )\left ( 1.6473 \right )\left ( 300\,K \right )=703.23\,K
Angle made by the reflected shock wave with the upper wall = \beta _{2}-\theta =46.75^{\circ}-20^{\circ}=26.75^{\circ}