The Kutta-Joukowski theorem {L}’=\rho _{\infty}V_{\infty}\tau was derived exactly for the case of the lifting cylinder. Implement a physical argument for this theorem.
Apply Kutta-joukowski theorem for a two dimensional body of arbitrary shape by making a physical argument.
Kutta-Joukowski theorem states Lift per unit span=density*velocity*circulation.
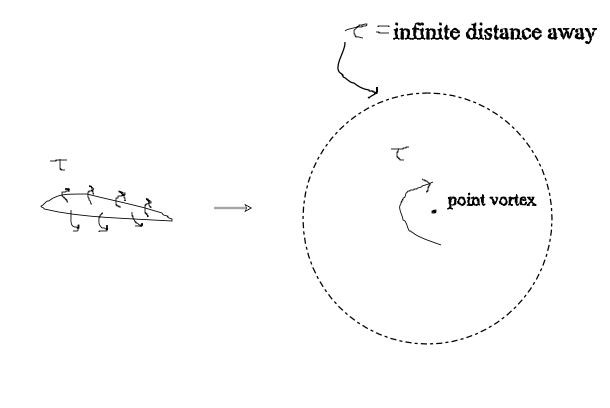
The flow over an airfoil can be synthesized by using point sources and vortices. The strength of the vortices, added together, gives the total circulation, τ, around the airfoil. This value of circulation is same along all closed curves around the airfoil even if closed curve is drawn away at a very large distance from the airfoil. In this case, the airfoil becomes a speck on the page, and the distributed point vortices appear as one stronger point vortex with strength τ. This is exactly equivalent to the single point vortex and the lift on the airfoil where the circulation is taken as the total ‘τ’ is the same,
Lift per unit span=density*velocity*circulation.