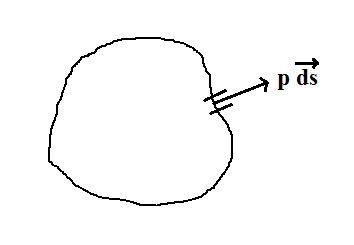
Consider a body of arbitrary shape. If the pressure distribution over the surface of the body is constant, prove that the resultant pressure force on the body is zero.
Consider a body of arbitrary shape. If the pressure distribution over the surface of the body is constant, prove that the resultant pressure force on the body is zero.
Here body is of arbitrary shape.
\vec{F}=-\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_s { p.\overrightarrow {ds} }
When p=p_{\infty}
\vec{F}=-p_{\infty}\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_s { \overrightarrow {ds} }
The integral of the surface vector over a closed surface is zero.That is
\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_s { \overrightarrow {ds} }=0
Therefore
\vec{F}=0