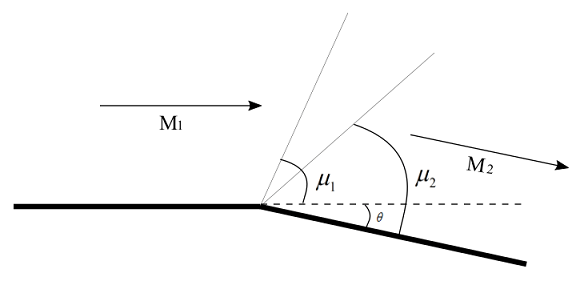
The upstream Mach number, pressure and temperature of a supersonic flow over an expansion corner having deflection angle \theta =25^{^{\circ}} is M_{1}=2.2,\,p_{1}=0.8\,atm and T_{1}=360\,K. Find the downstream Mach number, pressure, temperature, density , total pressure, total temperature, and the angles made by the forward and rearward Mach lines with local flow direction.
The upstream Mach number, pressure and temperature of a supersonic flow over an expansion corner having deflection angle \theta =25^{^{\circ}} is M_{1}=2.2,\,p_{1}=0.8\,atm and T_{1}=360\,K. Find the downstream Mach number, pressure, temperature, density , total pressure, total temperature, and the angles made by the forward and rearward Mach lines with local flow direction.
Downstream Mach number can be calculated from Prandtl-Meyer function
\nu (M)=\sqrt{\frac{\gamma +1}{\gamma -1}}tan^{-1}\sqrt{\frac{\gamma -1}{\gamma +1}\left ( M^{2}-1 \right )}-tan^{-1}\sqrt{M^{2}-1}
For a Mach number of 2.2, \nu \left ( M_{1} \right )=31.73^{^{\circ}}
\theta =\nu \left ( M_{2} \right )-\nu \left ( M_{1} \right )
\Rightarrow \nu \left ( M_{2} \right )=\theta + \nu \left ( M_{1} \right ) = 25^{\circ}+31.73^{\circ}=56.73^{\circ}
for, \nu \left ( M_{2} \right )=56.73^{^{\circ}}, Mach number M_{2}=3.389
From Isentropic flow properties for, M_{1}=2.2
\frac{p_{01}}{p_{1}}=10.69 and
\frac{T_{01}}{T_{1}}=1.968
For, M_{2}=3.389
\frac{p_{02}}{p_{2}}=65.0798 and
\frac{T_{02}}{T_{2}}=3.297
Total pressure and total temperature is constant through the expansion wave, so
p_{01}=p_{02} and T_{01}=T_{02}
Therefore,
p_{2}=\left ( \frac{p_{2}}{p_{02}} \right )\left ( \frac{p_{01}}{p_{1}} \right )p_{1}=\left ( \frac{1}{65.0798} \right )\left ( 10.69 \right )0.8=0.1314\,atm
T_{2}=\left ( \frac{T_{2}}{T_{02}} \right )\left ( \frac{T_{01}}{T_{1}} \right )T_{1}=\left ( \frac{1}{3.297} \right )\left ( 1.968 \right )360=214.886\,K
p_{2}=\rho _{2}RT_{2}
\Rightarrow 0.1314=\rho _{2}\left ( 287 \right )\left ( 214.886\,K \right )
\Rightarrow \rho _{2}=\frac{0.1314}{\left ( 287 \right )\left ( 214.886 \right )}=2.13\times 10^{-6}\,kg/m^{3}
Since,
p_{01}=p_{02}\Rightarrow p_{02}=\left ( \frac{p_{01}}{p_{1}} \right )\left ( p_{1} \right )=\left ( 10.69 \right )\left ( 0.8 \right )=8.552\,atm
Also,
T_{01}=T_{02}\Rightarrow T_{02}=\left ( \frac{T_{01}}{T_{1}} \right )\left ( T_{1} \right )=\left ( 1.968 \right )\left ( 360 \right )=708.48\,K
Mach angle is given by \mu = Sin^{-1}\left ( \frac{1}{M} \right )
Therefore Mach angle \mu _{1} made by upstream Mach wave for M_{1}=2.2 is 27.04^{\circ}
Mach angle \mu _{2} made by downstream Mach wave forM_{2}=3.389 is 17.16^{\circ}
and, angle made by forward Machline is 27.04^{\circ} and angle made by the rearward Machline is 17.16^{\circ}-25^{\circ}=-7.84^{\circ}