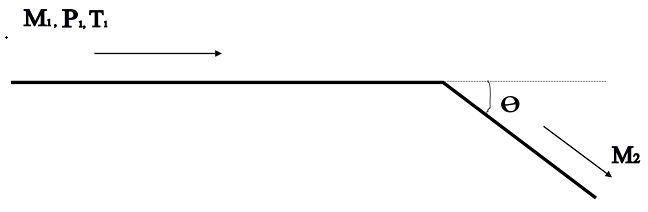
Consider the inviscid,adiabatic flow of air at free stream conditions \(M_{1}=2,P_{1}=1\;atm\) and \(T_{1}=288\;K\) around a sharp expansion corner \(\left ( \theta =20^{\circ} \right )\). Assume air to be calorically perfect with \(\gamma =1.4\). What is the Mach number \(M_{2}\), downstream of the expansion corner ?
Consider the inviscid,adiabatic flow of air at free stream conditions \(M_{1}=2,P_{1}=1\;atm\) and \(T_{1}=288\;K\) around a sharp expansion corner \(\left ( \theta =20^{\circ} \right )\) as shown below. The Prandtl-Meyer function \(\nu\), is given as a function of Mach number M , as
\[\nu (M)=\sqrt{\frac{\gamma +1}{\gamma -1}}tan^{-1}\sqrt{\frac{\gamma -1}{\gamma +1}\left ( M^{2} -1\right )}-tan^{-1}\sqrt{M^{2}-1}\]
Assume air to be calorically perfect with \(\gamma =1.4\) . What is the Mach number \(M_{2}\), downstream of the expansion corner ?
Prandtl-Meyer expansion theory tells that \[\theta =\nu \left ( M_{2} \right )-\nu \left ( M_{1} \right )\]
Here
\(\nu \left ( M_{1} \right )=\sqrt{\frac{2.4}{0.4}}tan^{-1}\sqrt{\frac{0.4}{2.4}\times 3}-tan^{-1}\sqrt{3}
\\=26.38^{\circ}\)
\(\nu \left ( M_{2} \right )=\theta +\nu \left ( M_{1} \right )
\\=20^{\circ}+26.38^{\circ}
\\=46.35^{\circ}\)
On putting the value of \(\nu (M_{2})\) in the Prandtl-Meyer function we get
\(46.35^{\circ}=\sqrt{\frac{2.4}{0.4}}tan^{-1}\sqrt{\frac{0.4}{2.4}\left ( M_{2}^{2}-1 \right )}-tan^{-1}\sqrt{M_{2}^{2}+1}\)
\(\Rightarrow M_{2}=2.83\) approximately.