Home

Write a matlab solution to Rankine nose problem.

Write a matlab solution to Rankine nose problem.

techAir Asked on 5th November 2019 in Aerodynamics.
Add Comment
Cancel
    • 1 Answer(s)

    The Rankine nose or Rankine leading edge is an example of flow around the leading edge of a symmetric aerodynamic body which is symmetric about the x-axis of coordinate system.This flow can be obtained by adding a uniform flow and a source flow at the origin.The velocity potential and stream function of this flow is

    \phi=U_{\infty}x+\frac{m}{4\pi}ln\left ( x^{2}+y^{2} \right )\;,\;\psi=U_{\infty}y+\frac{m}{2\pi}tan^{-1}\frac{y}{x}

    The velocity field for this flow is u=U_{\infty}+\frac{m}{2\pi}\frac{x}{x^{2}+y^{2}}\;;\;v=\frac{m}{2\pi}\frac{y}{x^{2}+y^{2}}

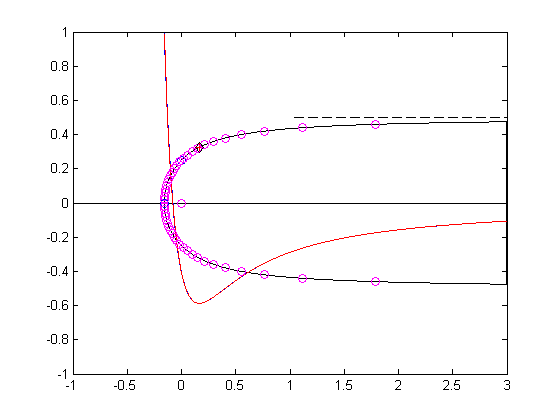
    Matlab solution to the problem is

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    clear;clc
    disp('Example: Rankine nose')
    m = 1; % Source strength for source at (x,y) = (0,0).
    V = 1; % Free stream velocity in the x-direction
    disp(' V m ')
    disp([V m])
    disp(' Velocity potential:')
    disp(' phi = V*x + (m/4/pi)*log(xˆ2+yˆ2)')
    disp('Stream function:')
    disp(' psi = V*y + (m/2/pi)*atan2(y,x)')
    disp('The (x,y) components of velocity (u,v):')
    disp(' u = V + m/2/pi * xc/(xˆ2+yˆ2)')
    disp(' v = m/2/pi * y/(xˆ2+yˆ2)')
    %
    xstg = - m/2/pi/V; ystg = 0; % Location of stagnation point.
    %
    N = 1000;
    xinf = 3;
    xd = xstg:xinf/N:xinf;
    for n = 1:length(xd)
    if n==1
    yd(1) = 0;
    else
    yd(n) = m/2/V;
    for it = 1:2000
    yd(n) = (m/2/V)*( 1 - 1/pi*atan2(yd(n),xd(n)) );
    end
    end
    end
    xL(1) = xd(end); yL = -yd(end);
    for nn = 2:length(xd)-1
    xL(nn) = xd(end-nn); yL(nn) = -yd(end-nn);end
    plot([xd xL],[yd yL],'k',[-1 3],[0 0],'k'),axis([-1 3 -1 1])
    u = V + m/2/pi * xd./(xd.^2+yd.^2);
    v = m/2/pi * yd./(xd.^2+yd.^2);
    Cp = 1 - (u.^2+v.^2)/V^2;
    hold on
    plot(xd,Cp),axis([-1 3 -1 1])
    plot(0,m/V/4,'o')
    plot(xstg,ystg,'o')
    plot([1 3],[m/2/V m/2/V],'--k')
    [Cpmin, ixd] = min(Cp);
    xmin = xd(ixd);
    ymin = yd(ixd);
    plot(xmin,ymin,'+r')
    Cpmin;
    % Computation of normal and tangential velocity on (xd,yd):
    phi = V*xd + (m/4/pi).*log(xd.^2+yd.^2);
    dx = diff(xd); dy = diff(yd); ds = sqrt(dx.^2 + dy.^2);
    dph = diff(phi); ut = dph./ds; xm = xd(1:end-1) + dx/2;
    psi = V*yd + (m/2/pi).*atan2(yd,xd);
    plot(xm,1-ut.^2/V^2,'r')
    %
    % Check on shape equation
    %
    th = 0:pi/25:2*pi;
    r = (m/2/pi/V)*(pi - th)./sin(th);
    xb = r.*cos(th);
    yb = r.*sin(th);
    plot(xb,yb,'om')
    %
    % Exact location of minimum pressure
    thm = 0;
    for nit = 1:1000
    thm = atan2(pi-thm,pi-thm-1);
    end
    thdegrees = thm*180/pi;
    rm = (m/2/pi/V)*(pi - thm)/sin(thm);
    xm = rm*cos(thm);
    ym = rm*sin(thm);
    plot(xm,ym,'dk')
    um = V + m/2/pi * xmin/(xmin^2+ymin^2);
    vm = m/2/pi * ymin/(xmin^2+ymin^2);
    Cpm = 1 - (um^2+vm^2)/V^2;

    Rankine nose solutionRankine nose solution

    Cancel
    Worldtech Answered on 5th November 2019.
    Add Comment
    Cancel

    • Your Answer

    By posting your answer, you agree to the privacy policy and terms of service.