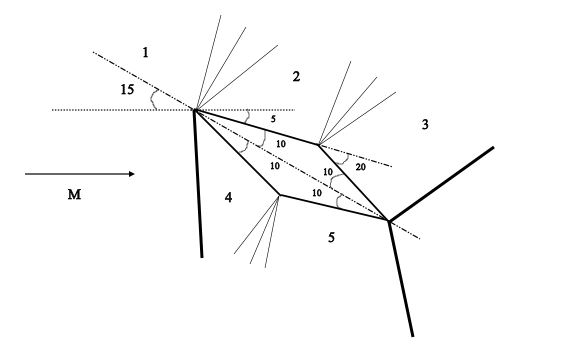
Consider a diamond-wedge airfoil, with a half angle of 10 degree. The airfoil is at an angle of attack of 15 degree to a Mach 3 free stream. Calculate the lift and wave-drag coefficients for the airfoil.
Consider a diamond-wedge airfoil, with a half angle of 10 degree. The airfoil is at an angle of attack of 15 degree to a Mach 3 free stream. Calculate the lift and wave-drag coefficients for the airfoil.
The diamond wedge airfoil is
We need to obtain Prandtl-Meyer function and Mach number \({M_2}\) for region 2 , here
\[\begin{array}{l}{\nu _1} = {49.76^ \circ }\\{\nu _2} = {\nu _1} + \theta \end{array}\]
This gives \({M_2} = 3.27\)
From Appendix A, Isentropic flow properties table, obtain the parameters at \({M_1} = 3\) and \({M_2} = 3.27\), for
\(\begin{array}{l}{M_1} = 3,\frac{{{P_{01}}}}{{{P_1}}} = 36.73\\{M_2} = 3.27,\frac{{{P_{02}}}}{{{P_2}}} = 54.76\end{array}\)
Also obtaining Prandtl-Meyer function and Mach number \({M_3}\)for region 3, here
\(\begin{array}{l}{\nu _3} = {\nu _2} + \theta \\ = {54.76^ \circ } + {20^ \circ }\\ = {74.76^ \circ }\\{\rm{therefore}}\,{M_3} = 4.78\end{array}\)
From Appendix A, isentropic flow properties table we need to obtain the pressure ratio at \({M_3} = 4.78\), for
\({M_3} = 4.78,\frac{{{P_{03}}}}{{{P_3}}} = 407.83\)
Now obtaining β, from θ-β-M relation and normal component of Mach number \({M_{n1}}\)
\(\begin{array}{l}\beta = {44^ \circ }\\{M_{n,1}} = {M_1}\sin \beta \\3\sin {44^ \circ }\\ = 2.08\end{array}\)
Also obtaining the parameters from Appendix B, normal shock wave properties table
\(\begin{array}{l}\frac{{{P_4}}}{{{P_1}}} = 4.801,\\{M_{n,4}} = 0.5643\\\frac{{{P_{04}}}}{{{P_1}}} = 0.6835\end{array}\)
Now obtain the Mach number\({M_4}\)
\(\begin{array}{l}{M_4} = \frac{{{M_{n,4}}}}{{\sin (\beta – \theta )}}\\ = \frac{{0.5643}}{{\sin ({{44}^ \circ } – {{25}^ \circ })}}\\ = 1.733\end{array}\)
From Appendix A, isentropic flow properties table on obtaining the pressure ratio at\({M_4} = 1.733\), for
\({M_4} = 1.733,\frac{{{P_{04}}}}{{{P_4}}} = 5.165\)
On obtain Prandtl-Meyer function and Mach number \({M_5}\)for region 5, here
\(\begin{array}{l}{\nu _5} = {\nu _4} + \theta \\ = {18.69^ \circ } + {20^ \circ }\\ = {38.69^ \circ }\\{\rm{therefore}}\,{M_5} = 2.48\end{array}\)
From Appendix A, isentropic flow properties table obtaining the pressure ratio at \({M_5} = 2.48\) , for
\(\begin{array}{l}{M_5} = 2.48\\\frac{{{P_{05}}}}{{{P_5}}} = 16.56\end{array}\)
Now Obtaining static pressure ratio at regions 2
\(\begin{array}{l}\frac{{{P_2}}}{{{P_1}}} = \frac{{{P_2}}}{{{P_{02}}}}\frac{{{P_{02}}}}{{{P_{01}}}}\frac{{{P_{01}}}}{{{P_1}}}\\ = \frac{1}{{54.76}} \times 1 \times 36.73\\ = 0.6706\end{array}\)
Obtaining static pressure ratio at region 3
\(\begin{array}{l}\frac{{{P_3}}}{{{P_1}}} = \frac{{{P_2}}}{{{P_1}}}\frac{{{P_3}}}{{{P_2}}} = \frac{{{P_2}}}{{{P_1}}}\frac{{{P_3}}}{{{P_{03}}}}\frac{{{P_{03}}}}{{{P_{02}}}}\frac{{{P_{02}}}}{{{P_2}}}\\ = 0.6707 \times \frac{1}{{407.83}} \times 1 \times 54.76\\ = 0.09\end{array}\)
Obtaining static pressure ratio at region 4
\(\frac{{{P_4}}}{{{P_1}}} = 4.881\)
Obtaining static pressure ratio at region 5
\(\begin{array}{l}\frac{{{P_4}}}{{{P_5}}} = \frac{{{P_5}}}{{{P_{05}}}}\frac{{{P_{05}}}}{{{P_{04}}}}\frac{{{P_{04}}}}{{{P_{01}}}}\frac{{{P_{01}}}}{{{P_1}}}\\ = \frac{1}{{16.56}} \times 1 \times 0.6835 \times 36.73\\ = 1.516\end{array}\)
Obtaining lift per unit span \(L^\prime \) considering length of each face as \(l\)
\(\begin{array}{l}{L^\prime} = {P_4}l\cos {25^ \circ } + {P_5}l\cos {5^ \circ } – {P_2}l\cos {5^ \circ } – {P_3}\cos {25^ \circ }\\{L^\prime} = \left( {{P_4} – {P_3}} \right)l\cos {25^ \circ }\\ = \frac{2}{{\gamma M_1^2}}\frac{l}{c}\left[ {\left( {\frac{{{P_4}}}{{{P_1}}} – \frac{{{P_3}}}{{{P_1}}}} \right)\cos {{25}^ \circ } + \left( {\frac{{{P_5}}}{{{P_1}}} – \frac{{{P_2}}}{{{P_1}}}} \right)\cos {5^ \circ }} \right]\end{array}\)
Obtaining coefficient of lift \({c_l}\)
\(\begin{array}{l}{c_l} = \frac{2}{{1.4 \times {3^2}}} \times \frac{l}{c} \times \left[ {\left( {4.881 – 0.09} \right)\cos {{25}^ \circ } + \left( {1.516 – 0.6707} \right)\cos {5^ \circ }} \right]\\{c_l} = 0.823\frac{l}{c}\\{\rm{since}}\,\frac{{c/2}}{l} = \cos {10^ \circ }\\{\rm{therefore}}\,\,\frac{l}{c} = \frac{1}{{2\cos {{10}^ \circ }}} = 0.5077\\{c_l} = 0.823 \times 0.5077\\ = \,0.418\end{array}\)
Obtaining drag per unit span \({D^\prime}\)
\(\begin{array}{l}{D^\prime} = {P_4}l\sin {25^ \circ } + {P_5}l\sin {5^ \circ } – {P_2}l\sin {5^ \circ } – {P_3}l\sin {25^ \circ }\\{D^\prime} = \left( {{P_4} – {P_3}} \right)l\sin {25^ \circ } + \left( {{P_5} – {P_2}} \right)l\sin {5^ \circ }\end{array}\)
Obtaining coefficient of drag \({c_d}\)
\(\begin{array}{l}{c_d} = \frac{{{D^\prime}}}{{{q_\infty }s}} = \frac{{{D^\prime}}}{{\frac{\gamma }{2}{P_1}M_1^2c}}\\ = \frac{2}{{\gamma M_1^2}}\frac{l}{c}\left[ {\left( {\frac{{{P_4}}}{{{P_1}}} – \frac{{{P_3}}}{{{P_1}}}} \right)\sin {{25}^ \circ } + \left( {\frac{{{P_5}}}{{{P_1}}} – \frac{{{P_2}}}{{{P_1}}}} \right)\sin {5^ \circ }} \right]\\ = \frac{2}{{1.4 \times {3^2}}} \times 0.5077 \times \left[ {\left( {4.881 – 0.09} \right)\sin {{25}^ \circ } + \left( {1.516 – 0.6707} \right)\sin {5^ \circ }} \right]\\ = \,0.169\end{array}\)
Wouldn’t region #2 have a theta = 5 deg instead of 20 deg, due to the upper surface of the diamond compensating 10 deg?