Find the circulation around a spinning circular cylinder in free stream flow of velocity 40\,m/s at a standard sea level conditions, if the lift produced by the cylinder is 8\,N/m of span.
Find the circulation around a spinning circular cylinder in free stream flow of velocity 40\,m/s at a standard sea level conditions, if the lift produced by the cylinder is 8\,N/m of span.
Lift per unit span produced by a circular cylinder with circulation, \tau, is L^\prime=\rho _{\infty} v_{\infty }\tau This is also called the Kutta-Joukowski theorem. A spinning cylinder has a higher velocity at the top surface and a lower velocity at the bottom surface. Therefore, pressure at the top surface of the cylinder is lower than the bottom. This pressure difference creates a net upward force, which is called lift.
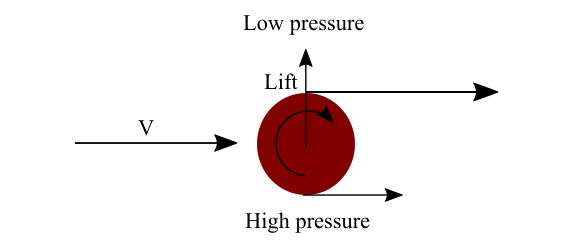 Lift produced on spinning cylinder
Lift produced on spinning cylinder




