Find the gliding distance of an aircraft flying at an altitude of 1500\,m with a maximum lift to drag ratio of 8.
Find the gliding distance of an aircraft flying at an altitude of 1500\,m with a maximum lift to drag ratio of 8.
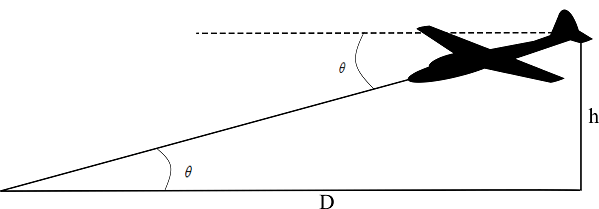
Aircraft starts to glide at an altitude of 1500\,m.
From the figure,
\tan \theta = \frac{h}{D} \Rightarrow D = \frac{h}{{\tan \theta }}
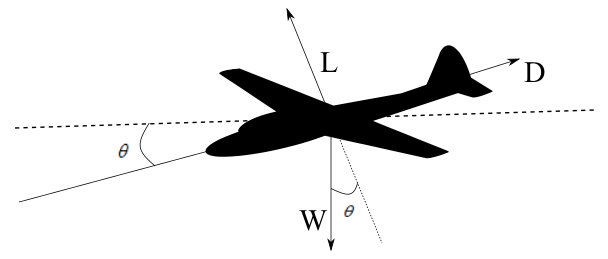
For the unaccelerated glide, in equilibrium L = W\cos \theta , D = W\sin \theta ,
\Rightarrow \left( {\frac{L}{D}} \right) = \frac{{W\cos \theta }}{{W\sin \theta }} = \left( {\frac{1}{{\tan \theta }}} \right)
On putting the values , to calculate the distance
D = \frac{h}{{\tan \theta }} = h\left( {\frac{L}{D}} \right) = 1500 \times 8 = 12000\,m