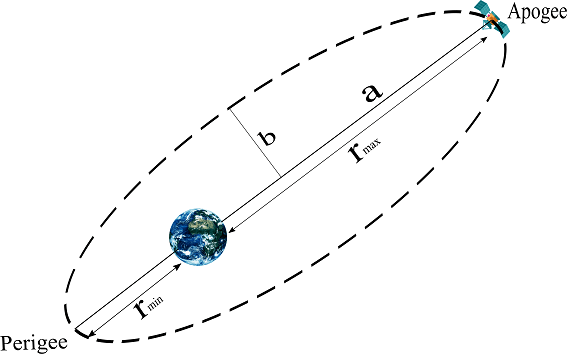
A communication satellite orbiting around earth has an eccentricity of 0.0014. Find the time period of the satellite, altitude at apogee and velocity at perigee, if the satellite has an altitude of 400\,km at perigee from the surface of the earth.
A communication satellite orbiting around earth has an eccentricity of 0.0014. Find the time period of the satellite, altitude at apogee and velocity at perigee, if the satellite has an altitude of 400\,km at perigee from the surface of the earth.
\frac{{{r_{\max }}}}{{{r_{\min }}}} = \frac{{1 + e}}{{1 – e}} = \frac{{1 + 0.0014}}{{1 – 0.0014}} = 1.0028
\Rightarrow {r_{\max }} = {r_{\min }}\left( {1.0028} \right)
{r_{\min }} = {\rm{radius}}\,{\rm{of}}\,{\rm{earth}}\,{\rm{ + }}\,{\rm{altitude}}\,{\rm{above}}\,{\rm{earth’s}}\,{\rm{surface}}
\Rightarrow {{\rm{r}}_{\min }} = 6.4 \times {10^6} + 0.4 \times {10^6} = 6.8 \times {10^6}\,m
\Rightarrow {r_{\max }} = 6.8 \times {10^6}\left( {1.0028} \right) = 681904\,m = 6.81904 \times {10^6}\,m
Therefore satellite’s altitude at apogee is
6.81904 \times {10^6} – 6.4 \times {10^6} = 419040\,m = 419.04\,km
Time period of the satellite is given as
{T^2} = \frac{{4{\pi ^2}}}{{{k^2}}}{a^3}
{k^2} = G{M_{earth}} = 3.986 \times {10^{14}}\,{m^3}/{s^2}
\Rightarrow a = {\rm{semi}}\,{\rm{major}}\,{\rm{axis}}\,{\rm{ = }}\frac{{{r_{\max }} + {r_{\min }}}}{2} = \frac{{6.81904 \times {{10}^6} + 6.8 \times {{10}^6}}}{2} = 6.80952 \times {10^6}\,m
{T^2} = \frac{{4{\pi ^2}}}{{3.986 \times {{10}^{14}}}} \times {\left( {6.80952 \times {{10}^6}} \right)^3}
\Rightarrow T = 5592.242\,s = 1.5534\,hr
{V_{perigee}} = {r_{\min }}\dot \theta
\dot \theta = \frac{h}{{{{\left( {{r_{\min }}} \right)}^2}}}
{h^2} = {r_{\min }}\left( {1 + e} \right){k^2}
\Rightarrow {h^2} = \left( {6.8 \times {{10}^6}} \right)\left( {1 + 0.0014} \right)3.986 \times {10^{14}}
\Rightarrow h = 5.20987 \times {10^{10}}
Therefore,
\dot \theta = \frac{{5.20987 \times {{10}^{10}}}}{{{{\left( {6.8 \times {{10}^6}} \right)}^2}}} = 0.0011267\,rad/s
{V_{perigee}} = \left( {6.8 \times {{10}^6} \times 0.0011267} \right) = 7661.56\,m/s = 7.66156\,km/s