Find the velocity of an airplane flying at a standard sea level, if the static pressure at the throat of venturi is \(100 000 N/m^{2}\).
Find the velocity of an airplane flying at a standard sea level, if the static pressure at the throat of venturi is \(100 000 N/m^{2}\).
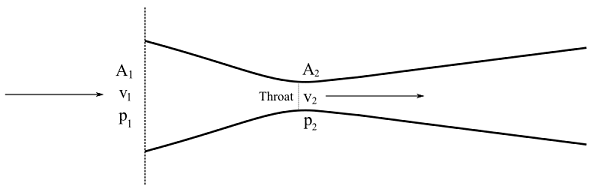
A venturi is a device which is used to measure the airspeed. It is a converging diverging duct. The inlet pressure and velocity of the duct is \(p_{1}\) and \(v_{1}\). At the throat of the duct velocity increases to the maximum, \(v_{2}\) and pressure decrease to minimum, \(p_{2}\). In the divergent section of the duct, velocity decreases and pressure increases. The inlet and throat area of the duct are \(A_{1}\) and \(A_{2}\).
Velocity of air is calculated using Bernoulli’s equation, which is\[v_{1}=\sqrt{\frac{2\left ( p_{1} – p_{2} \right )}{\rho \left [ \left ( \frac{A_{1}}{A_{2}} \right )^{2}-1\right ]}}\] Here, \(p_{1}\) is the atmospheric pressure, which is \(101325\,N/m^{2}\), \(p_{2}=100000\,N/m^{2}\),\(\frac{A_{2}}{A_{1}} = 0.8\).On putting the values, \[v_{1}=\sqrt{\frac{2\left ( 101325-100000 \right )}{1.225\left [ \left ( \frac{1}{0.8} \right )^{2}-1\right ]}}\]\[\Rightarrow v_{1}=62.015\,m/s\]Therefore, velocity of the airplane is \(62.015\,m/s\).