An aircraft in flight, produces wing tip vortices. Low pressure is created on the top surface and a high pressure is created on the bottom surface. This difference in pressure leads to air flow at the wing tips creating a circulatory motion which trails down stream of the wing. These are called vortex.

These wing tip vortices creates downwash which results in induced drag.

Induced drag can be calculated as \[{D_i} = L\sin {\alpha _i}\] where \(L\) is the lift. Since induced angle of attack \({\alpha _i}\) is small. Therefore,\[{D_i} = L{\alpha _i}\]

Elliptical wing planform

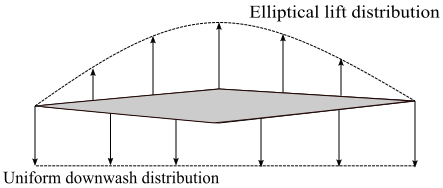
For an elliptical wing, lift per unit span varies elliptically along its span, and has a uniform downwash distribution. Induced angle of attack for the elliptical wing, from incompressible flow theory is \[{\alpha _i} = \frac{{{C_L}}}{{\pi AR}}\]

Therefore induced drag will be\[{D_i} = L{\alpha _i} = L \times \frac{{{C_L}}}{{\pi AR}}\]

and coefficient of induced drag will be \[{C_{D,i}} = \frac{{C_L^2}}{{\pi AR}}\]

For all general wings a span efficiency factor, \(e\) is defined such that \[{C_{D,i}} = \frac{{C_L^2}}{{\pi eAR}}\]

and \(e <= 1\). Span efficiency factor, \( e \), comes from the calculation of coefficient of induced drag from the Prandtl’s classical lifting line theory. For all general planform wings \(e\) is less than 1. For an elliptical wing, \(e=1\). Therefore, induced drag is minimum for an elliptical wing planform. For a typical subsonic airplane, \(e\) is between 0.85 to 0.95, therefore for such airplane aspect ratio is increased to minimise the induced drag.

An elliptical wing planform aircraft

An elliptical wing planform is expensive to make, for such a tapered wing with an approximate elliptical lift distribution is made. Induced drag coefficient for an tapered wing with straight leading and trailing edges has a minimum value and are easier to produce.