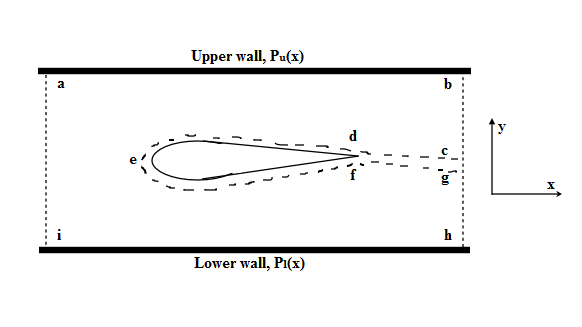
Consider an airfoil in a wind tunnel (i.e. a wing that spans the entire test section). Prove that the lift per unit span can be obtained from the pressure distributions on the top and bottom walls of the wind tunnel (i.e., from the pressure distributions on the walls above and below the airfoil).
Consider an airfoil in a wind tunnel (i.e., a wing that spans the entire test section). Prove that the lift per unit span can be obtained from the pressure distributions on the top and bottom walls of the wind tunnel (i.e., from the pressure distributions on the walls above and below the airfoil).
We denote the pressure distributions over the upper and lower walls by p_{u}(x) and p_{l}(x) respectively.
p=p_{\infty} and v=0 (Assuming faces ai and bh are far enough upstream and downstream of the model such that p=p_{\infty} and v=0)
L = – \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_s {\left( {\rho \overrightarrow {v} \cdot \overrightarrow {ds} } \right)} v \; – \iint\limits_{abhi} {\left( {p\overrightarrow {ds} } \right)}y
Here first integral = 0 , because \vec{v}\cdot \vec{ds}=0 or because v=0.
Therefore {L^\prime } = – \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{abhi} {\left( {p\overrightarrow {ds} } \right)} y = – \left[ {\int_a^b {{p_u}dx \;- \int\limits_i^h {{p_l}dx} } } \right]
\Rightarrow{L^\prime } = \left[ {\int_i^h {{p_l}dx \;- \int\limits_a^b {{p_u}dx} } } \right] = 0