Velocity potential and stream function for a source flow is given as $\phi=\frac{\Lambda }{2\pi}ln\;r$ and $\psi=\frac{\Lambda }{2\pi}\;\theta$.

  $$\phi=\frac{\Lambda }{2\pi}ln\;r \\\frac{\partial \phi}{\partial r}=\frac{\Lambda }{2\pi}\frac{1}{r}\;,\;\frac{\partial^2 \phi}{\partial r^2}=-\frac{\Lambda }{2\pi}\frac{1}{r^{2}} \\\frac{\partial \phi}{\partial \theta}=0\;;\;\frac{\partial^2 \phi}{\partial \theta^2}=0$$

Therefore Laplace equation $$\frac{1}{r}\frac{\partial }{\partial r}\left ( r\; \frac{\partial \phi}{\partial r} \right )+\frac{1}{r^{2}}\frac{\partial^2 \phi}{\partial \theta^2}=0+0=0$$

is satisfied.

$$\psi=\frac{\Lambda }{2\pi}\theta$$ $$\frac{\partial \psi}{\partial r}=0\;;\;\frac{\partial^2 \psi}{\partial r^2}=0 \\\frac{\partial \psi}{\partial \theta}=\frac{\Lambda }{2\pi}\;;\;\frac{\partial^2 \psi}{\partial \theta^2}=0$$

Therefore Laplace equation $$\frac{1}{r}\frac{\partial }{\partial r}\left ( r\;\frac{\partial \psi}{\partial r} \right )+\frac{1}{r^{2}}\frac{\partial^2 \psi}{\partial \theta^2}=\frac{1}{r}\frac{\partial (0)}{\partial r}+\frac{1}{r^{2}}\left ( 0 \right )=0+0=0$$

is satisfied.

We  need to find here the velocity of the airplane. $$P_{0}=P_{\infty}+\frac{1}{2}\rho V_{\infty}^{2} \\\Rightarrow V_{\infty}=\sqrt{\frac{2\left ( P_{0}-P_{\infty} \right )}{\rho }} \\=\sqrt{\frac{2\left ( 1.07-1.01 \right )\times 10^{5}}{1.23}} \\=98.8\;m/s$$

Venturi has a throat area ratio of 0.85.We need to calculate here the maximum vacuum obtainable in the reservoir when the venturi is placed in an airstream of $90\;m/s$.

$$P_{1}-P_{2}=\frac{1}{2}\rho V_{1}^{2}\left [ \left ( \frac{A_{1}}{A_{2}} \right )^{2}-1 \right ] \\=\frac{1}{2}\left ( 1.23 \right )\left ( 90 \right )^{2}\left [ \left ( \frac{1}{0.85} \right )^{2}-1 \right ] \\=1913\;N/m^{2}$$

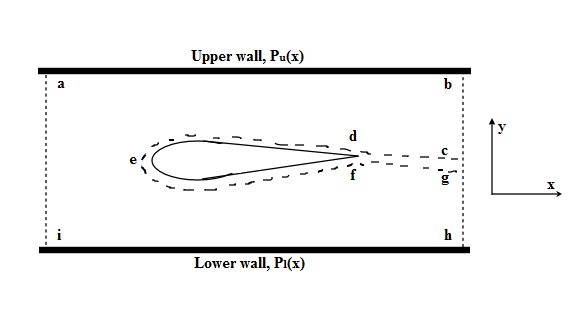
We denote the pressure distributions over the upper and lower walls by $p_{u}(x)$ and $p_{l}(x)$ respectively.

Figure : Wind Tunnel

$p=p_{\infty}$ and $v=0$ (Assuming faces $ai$ and $bh$ are far enough upstream and downstream of the model such that $p=p_{\infty}$ and $v=0$)

$$L = – \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_s {\left( {\rho \overrightarrow {v} \cdot \overrightarrow {ds} } \right)} v \; – \iint\limits_{abhi} {\left( {p\overrightarrow {ds} } \right)}y$$

Here first integral = 0 , because $\vec{v}\cdot \vec{ds}=0$ or because $v=0$.

Therefore $${L^\prime } = – \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{abhi} {\left( {p\overrightarrow {ds} } \right)} y = – \left[ {\int_a^b {{p_u}dx \;- \int\limits_i^h {{p_l}dx} } } \right]$$

$$\Rightarrow{L^\prime } = \left[ {\int_i^h {{p_l}dx \;- \int\limits_a^b {{p_u}dx} } } \right] = 0$$

$x$ and $y$ components of velocity are given by $u=cx$ and $v=-cy$.We need to calculate the stream function and velocity potential.Here

$$u=cx \\\frac{\partial \psi }{\partial y}=cx \\\Rightarrow \partial \psi=cx\partial y \\\Rightarrow \psi=cxy+f(x) \\v=-cy=-\frac{\partial \psi}{\partial x} \\\Rightarrow \psi=cxy+f(y)$$

Here f(x) and f(y) are constants:

$$\psi=cxy+const. \\u=cx=\frac{d\phi}{dx} \\\Rightarrow d\phi=cxdx \\\Rightarrow \phi=cx^{2}+f(y) \\v=-cy=\frac{\partial \phi}{\partial y}:\phi=-cy^{2}+f(x)$$

Therefore $$f(y)=-cy^{2}\;and \;f(x)=cx^{2}$$

and $$\phi=c\left ( x^{2}-y^{2} \right ) \\\psi=cxy+const.$$

Differentiating the above equation of $\psi$ with respect to ‘$x$’, holding $\psi=constant$

$$\frac{\partial \psi}{\partial x}=cx\frac{dy}{dx}+cy$$

or $$\left ( \frac{dy}{dx} \right )_{\psi=constant}=\left ( \frac{-y}{x} \right )$$

Differentiating the above equation of $\phi$ with respect to ‘$x$’,holding $\phi=constant$

$$0=2cx-2cy\left ( \frac{dy}{dx} \right )$$

or $$\left ( \frac{dy}{dx} \right )_{\phi=constant}=\left ( \frac{x}{y} \right )$$

On comparing the above equations we get $$\left ( \frac{dy}{dx} \right )_{\psi=constant}=\frac{-1}{\left (\frac{dy}{dx} \right )_{\phi=constant}}$$

Therefore the lines of constant $\phi$ are perpendicular to the lines of constant $\psi$.

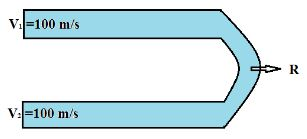
Length of the pipe is bent into ‘U’ shape.Here inside diameter = $0.5 \;m$ and air density = $1.23\;kg/m^{3}$.

Figure

‘-R’ exerted by the pipe, reverses the flow velocity.Cross sectional area =$\frac{\pi\;d^{2}}{4}$

$$A=\frac{\pi d^{2}}{4} \\=\frac{\pi (0.5)^{2}}{4} \\=0.196\;m^{2}$$

Mass flow entering the pipe is $$\dot{m}=\rho _{1}A_{1}V_{1}=1.23\times 0.196\times 100 \\=24.11\;kg/sec \\R=-\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}  \left ( \rho V\cdot ds \right )V \\V_{2}=-V_{1} \\R=-\left [ -\dot{m} V_{1}+\dot{m}V_{2}\right ]=\dot{m}\left ( V_{1}-V_{2} \right ) \\=\dot{m}\left [ V_{1}-\left ( -V_{1} \right ) \right ]=\dot{m}2V_{1} \\R=24.11\times 2\times 100 \\=4822\;N$$

a) Let for a vortex flow $u=\frac{cy}{x^{2}+y^{2}}$ and $v=\frac{-cx}{x^{2}+y^{2}}$.In polar coordinates the time rate of change of a fluid element per unit volume is given as $$\nabla\cdot \vec{V}=\frac{1}{r}\frac{\partial }{\partial r}\left ( rV_{r} \right )+\frac{1}{r}\frac{\partial V_{\theta}}{\partial \theta}$$

The velocity component  is transformed by using $x=rcos\theta$ and $y=rsin\theta$.

$$V_{r}=ucos\theta+vsin\theta \\V_{\theta}=-usin\theta+vcos\theta$$

$$u=\frac{cy}{x^{2}+y^{2}}=\frac{crsin\theta}{r^{2}}=\frac{c sin\theta}{r} \\v=\frac{-cx}{x^{2}+y^{2}}=\frac{crcos\theta}{r^{2}}=\frac{-c cos\theta}{r} \\V_{r}=\frac{c}{r}cos\theta sin\theta-\frac{c}{r}cos\theta sin\theta=0 \\V_{\theta}=\frac{-c}{r}sin^{2}\theta-\frac{c}{r}cos^{2}\theta=\frac{-c}{r}$$

$$\nabla\cdot \vec{V}=\frac{1}{r}\frac{\partial }{\partial r}\left ( 0 \right )+\frac{1}{r}\frac{\partial }{\partial \theta}\left ( \frac{-c}{r} \right )=0+0=0$$

b) The vorticity

Vorticity is given as $$\nabla \times \vec{V}=\vec{e_{z}}\left [ \frac{\partial }{\partial r}\left ( \frac{-c}{r} \right )-\frac{c}{r^{2}}-\frac{1}{r}\frac{\partial (0)}{\partial \theta} \right ] \\=\vec{e_{z}}\left [ \frac{c}{r^{2}}-\frac{c}{r^{2}} -0\right ] \\=0$$

Here $\nabla \times \vec{V}=0$ except at origin, where r=0.The flow field is singular at the origin.

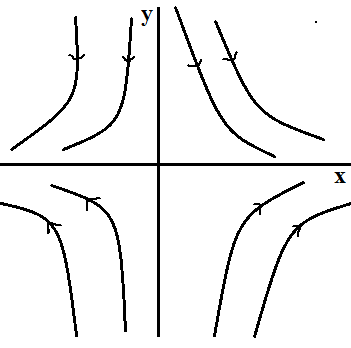
Here $u=cx$ and $v=-cy$.Since $$vdx – udy=0$$

Therefore $$\frac{dy}{dx}=\frac{v}{u}=\frac{-y}{x} \\\Rightarrow \frac{dy}{y}=\frac{-dx}{x}$$

On integrating $$ln(y)=xln(x)+C_{1} \\\Rightarrow y=\frac{C_{2}}{x}$$

These streamlines are in hyperbola shape.

Figure

Here $x$ and $y$ components of velocities are given.We need to find equation of streamlines. $$vdx-udy=0 \\\frac{dy}{dx}=\frac{v}{u}=\frac{-cx}{x^{2}+y^{2}}\times \frac{x^{2}+y^{2}}{cy}=\frac{-x}{y} \\\Rightarrow \frac{dy}{dx}=\frac{-x}{y} \\\Rightarrow ydy=-xdx$$

On integrating we get $$\Rightarrow \frac{y^{2}}{2}=\frac{-x^{2}}{2}+C \\\Rightarrow x^{2}+y^{2}=4C \\\Rightarrow x^{2}+y^{2}=C_{1}$$

Therefore streamlines are concentric with their centres at the origin.

Here $x$ component of velocity is $u=\frac{cx}{x^{2}+y^{2}}$ and $y$ component of velocity is $v=\frac{cy}{x^{2}+y^{2}}$ $$vdx-udy=0$$
$\Rightarrow vdx=udy \\\Rightarrow \frac{dy}{dx}=\frac{v}{u}=\frac{\frac{cy}{x^{2}+y^{2}}}{\frac{cx}{x^{2}+y^{2}}}=\frac{y}{x} \\\Rightarrow \frac{dy}{dx}=\frac{y}{x}=\frac{dy}{y}=\frac{dx}{x}$

On integrating

$ln(y)=ln(x)+C \\\Rightarrow ln\left ( \frac{y}{x} \right )=C \\\Rightarrow y=e^{C}x \\\Rightarrow y=xC_{1}$

Therefore streamlines are straight lines originating from the origin.